题目内容
1.若一个圆的圆心是抛物线x2=4y的焦点,且该圆与直线y=x+3相切,则该圆的标准方程是x2+(y-1)2=2.分析 求出抛物线的焦点即圆心坐标,利用切线的性质计算点C到切线的距离即为半径,从而得出圆的方程.
解答 解:抛物线的标准方程为:x2=4y,
∴抛物线的焦点为F(0,1).即圆C的圆心为C(0,1).
∵圆C与直线y=x+3相切,∴圆C的半径为点C到直线y=x+3的距离d=$\frac{|0-1+3|}{\sqrt{2}}$=$\sqrt{2}$.
∴圆C的方程为x2+(y-1)2=2.
故答案为:x2+(y-1)2=2.
点评 本题考查了抛物线的性质,圆的标准方程,属于基础题.

练习册系列答案
相关题目
9.若函数$f(x)=sinx(sinx-\sqrt{3}cosx)$的图象向左平移$\frac{π}{12}$个单位,得到函数g(x)的图象,则下列关于g(x)叙述正确的是( )
| A. | g(x)的最小正周期为2π | B. | g(x)在$[{-\frac{π}{8},\frac{3π}{8}}]$内单调递增 | ||
| C. | g(x)的图象关于$x=\frac{π}{12}$对称 | D. | g(x)的图象关于$(-\frac{π}{8},0)$对称 |
16.已知双曲线C$:\frac{x^2}{a^2}-\frac{y^2}{4}=1$的一条渐近线方程为2x+3y=0,F1,F2分别是双曲线C的左,右焦点,点P在双曲线C上,且|PF1|=2,则|PF2|等于( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
3.若直线l的一个方向向量为$\overrightarrow{a}$=(2,5,7),平面α的一个法向量为$\overrightarrow{μ}$=(1,1,-1),则( )
| A. | l∥α | B. | l⊥α | C. | l?α | D. | A、C都有可能 |
10.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,过点F2倾斜角为$\frac{π}{6}$的直线与双曲线的左支交于M点,且满足($\overrightarrow{{F}_{1}M}$+$\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{M{F}_{2}}$=0,则双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}+1}{2}$ |
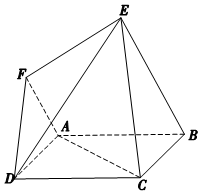 如图,正方形ABCD的边长等于2,平面ABCD⊥平面ABEF,AF∥BE,BE=2AF=2,EF=$\sqrt{3}$.
如图,正方形ABCD的边长等于2,平面ABCD⊥平面ABEF,AF∥BE,BE=2AF=2,EF=$\sqrt{3}$. 如图,已知四棱锥P-ABCD的底面是菱形,对角线AC,BD交于点O,OA=4,OB=3,OP=4,OP⊥底面ABCD,设点M满足$\overrightarrow{PM}$=$\frac{1}{2}$$\overrightarrow{MC}$.
如图,已知四棱锥P-ABCD的底面是菱形,对角线AC,BD交于点O,OA=4,OB=3,OP=4,OP⊥底面ABCD,设点M满足$\overrightarrow{PM}$=$\frac{1}{2}$$\overrightarrow{MC}$.