题目内容
在△ABC中,a,b,c分别为内角A,B,C的对边,面积S=
abcosC
(1)求角C的大小;
(2)设函数f(x)=
sin
cos
+cos2
,求f(B)的最大值,及取得最大值时角B的值.
| ||
| 2 |
(1)求角C的大小;
(2)设函数f(x)=
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
考点:正弦定理,三角函数中的恒等变换应用
专题:解三角形
分析:(1)利用三角形面积公式和已知等式,整理可求得tanC的值,进而求得C.
(2)利用两角和公示和二倍角公式化简整理函数解析式,利用B的范围和三角函数性质求得函数最大值.
(2)利用两角和公示和二倍角公式化简整理函数解析式,利用B的范围和三角函数性质求得函数最大值.
解答:
解:(1)由S=
absinC及题设条件得
absinC=
abcosC,
即sinC=
cosC,
∴tanC=
,
0<C<π,
∴C=
,
(2)f(x)=
sin
cos
+cos2
=
sinx+
cosx+
=sin(x+
)+
,
∵C=
,
∴B∈(0,
),
∴
<B+
<
当B+
=
,即B=
时,f(B)有最大值是
.
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
即sinC=
| 3 |
∴tanC=
| 3 |
0<C<π,
∴C=
| π |
| 3 |
(2)f(x)=
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∵C=
| π |
| 3 |
∴B∈(0,
| 2π |
| 3 |
∴
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
当B+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| 3 |
| 2 |
点评:本题主要考查了正弦定理的运用,三角函数恒等变换的应用.解题的过程中注意利用C的值确定B的范围这一隐形条件.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
执行如图所示的程序框图,则输出结果S的值为( )


A、
| ||
| B、0 | ||
C、-
| ||
| D、-1 |
 已知a为执行如图所示的程序框图输出的结果,又在数列{an}中,a1=1,an+1=2an+a,则( )
已知a为执行如图所示的程序框图输出的结果,又在数列{an}中,a1=1,an+1=2an+a,则( )A、an=
| ||||
B、an=2n-2+
| ||||
| C、an=3•2n-1-2 | ||||
| D、an=-2n+3 |
已知
=i(a,b∈R),其中i为虚数单位,则a2+b2=( )
| a+i |
| b+i |
| A、2 | B、3 | C、4 | D、5 |
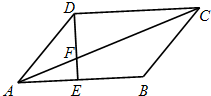 如图,平行四边形ABCD中,AE:EB=1:2,若△AEF的面积等于1cm2 则△CDF的面积等于
如图,平行四边形ABCD中,AE:EB=1:2,若△AEF的面积等于1cm2 则△CDF的面积等于