题目内容
已知数列{an}为等差数列,且公差不为0,{bn}为等比数列,a1=b1=1,a2=b2,a4=b3.
(Ⅰ)求{an}的通项公式.
(Ⅱ)设cn=n2an,其前n项和为Sn,求证:3≤
+
+…+
<4.
(Ⅰ)求{an}的通项公式.
(Ⅱ)设cn=n2an,其前n项和为Sn,求证:3≤
| 3 |
| S1 |
| 5 |
| S2 |
| 2n+1 |
| Sn |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由题意推导出(1+d)2=1+3d,解得d=1.由此能求出{an}的通项公式.
(Ⅱ)依题意cn=n2an=n3,从而得到Sn=
n2(n+1)2,由此利用裂项求和法和放缩法能证明3≤
+
+…+
<4.
(Ⅱ)依题意cn=n2an=n3,从而得到Sn=
| 1 |
| 4 |
| 3 |
| S1 |
| 5 |
| S2 |
| 2n+1 |
| Sn |
解答:
(Ⅰ)解:设等差数列的公差为d,
则由题意知a2=1+d,a4=1+3d….(2分)
∵{bn}为等比数列,a1=b1=1,a2=b2,a4=b3,
∴a22=a1•a4,
即(1+d)2=1+3d…(4分)
整理,得d2=d,又d≠0,解得d=1.…(5分)
∴an=1+(n-1)=n.…(6分)
(Ⅱ)证明:依题意cn=n2an=n3.(7分)
∴Sn=c1+c2+…+cn
=13+23+…+n3=
n2(n+1)2….(8分)
∴
=
=4
=4(
-
)….(10分)
∴
+
+…+
<4(
-
)+4(
-
)+…+4(
-
)
=4(1-
)<4….(12分)
∵
>0,∴
+
+…+
≥
=3
综上所述:3≤
+
+…+
<4…..(14分)
则由题意知a2=1+d,a4=1+3d….(2分)
∵{bn}为等比数列,a1=b1=1,a2=b2,a4=b3,
∴a22=a1•a4,
即(1+d)2=1+3d…(4分)
整理,得d2=d,又d≠0,解得d=1.…(5分)
∴an=1+(n-1)=n.…(6分)
(Ⅱ)证明:依题意cn=n2an=n3.(7分)
∴Sn=c1+c2+…+cn
=13+23+…+n3=
| 1 |
| 4 |
∴
| 2n+1 |
| Sn |
| 4(2n+1) |
| n2(n+1)2 |
| (n+1)2-n2 |
| n2(n+1)2 |
| 1 |
| n2 |
| 1 |
| (n+1)2 |
∴
| 3 |
| S1 |
| 5 |
| S2 |
| 2n+1 |
| Sn |
| 1 |
| 12 |
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| (n+1)2 |
=4(1-
| 1 |
| (n+1)2 |
∵
| 2n+1 |
| Sn |
| 3 |
| S1 |
| 5 |
| S2 |
| 2n+1 |
| Sn |
| 3 |
| S1 |
综上所述:3≤
| 3 |
| S1 |
| 5 |
| S2 |
| 2n+1 |
| Sn |
点评:本题主要考查等差数列、等比数列的通项公式,考查考生分析问题、解决问题的能力.对于第(Ⅰ)问,由已知条件递推关系可求出公差d,进而可求出{an},{bn}的通项公式;对于第(Ⅱ)问考察裂项求和法的合理运用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
已知集合M是满足下列性质的函数f(x)的集合:存在非零常数k,对定义域中的任意x,等式f(kx)=
+f(x)恒成立.现有两个函数:f(x)=ax+b(a≠0),g(x)=log2x,则函数f(x)、g(x)与集合M的关系为( )
| k |
| 2 |
| A、f(x)∈M,g(x)∈M |
| B、f(x)∉M,g(x)∈M |
| C、f(x)∈M,g(x)∉M |
| D、f(x)∉M,g(x)∉M |
 一个算法的程序框图如图所示,若该程序输出的结果为12,则判断框中应填入的条件是( )
一个算法的程序框图如图所示,若该程序输出的结果为12,则判断框中应填入的条件是( )| A、k≤4 | B、k≤3 |
| C、k<3 | D、k≥3 |
下列函数中,既是偶函数且值域为(-∞,0]的函数是( )
| A、f(x)=xsinx |
| B、f(x)=-2-x |
| C、f(x)=ln|x| |
| D、f(x)=-x2 |
已知{an}为等比数列,公比为q,若a2•a3=2a1,且a4与2a7的等差中项为
,则q=( )
| 5 |
| 4 |
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
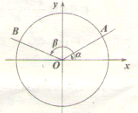 如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=
如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=