题目内容
已知数列{an}是等差数列,a2=6,a5=18,数列{bn}的前n项和为Sn,且Sn+
bn=1.
(1)求数列{an}的通项公式;
(2)记cn=an•bn,若cn+m≤0对任意的n∈N+恒成立,求实数m的取值范围.
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)记cn=an•bn,若cn+m≤0对任意的n∈N+恒成立,求实数m的取值范围.
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:(1)设an的公差为d,根据等差数列通项公式根据a2=6,a5=18可求得a1和d,进而可求得数列{an}的通项公式;
(2)先证明数列{bn}是以
为首项,
为公比的等比数列,求得数列{bn}的通项公式,进而可得{cn}的通项公式,求出n=1时,cn取到最大值
,即可求实数m的取值范围.
(2)先证明数列{bn}是以
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
解答:
解:(1)设an的公差为d,则:a2=a1+d,a5=a1+4d,
∵a2=6,a5=18,
∴a1+d=6,a1+4d=18,∴a1=2,d=4.
∴an=2+4(n-1)=4n-2.
(2)当n=1时,b1=S1,由S1+
b1=1,可得b1=
当n≥2时,∵Sn+
bn=1,Sn-1+
bn-1=1,
∴两式相减,整理可得bn=
bn-1,
∴数列{bn}是以
为首项,
为公比的等比数列,
∴bn=
,
∴cn=an•bn=
,
∴cn+1-cn=
,
∴n≥1,
∴cn+1≤cn,
∴n=1时,cn取到最大值
,
∵cn+m≤0对任意的n∈N+恒成立,
∴
+m≤0,
∴m≤-
.
∵a2=6,a5=18,
∴a1+d=6,a1+4d=18,∴a1=2,d=4.
∴an=2+4(n-1)=4n-2.
(2)当n=1时,b1=S1,由S1+
| 1 |
| 2 |
| 2 |
| 3 |
当n≥2时,∵Sn+
| 1 |
| 2 |
| 1 |
| 2 |
∴两式相减,整理可得bn=
| 1 |
| 3 |
∴数列{bn}是以
| 2 |
| 3 |
| 1 |
| 3 |
∴bn=
| 2 |
| 3n |
∴cn=an•bn=
| 4(2n-1) |
| 3n |
∴cn+1-cn=
| 16(1-n) |
| 3n+1 |
∴n≥1,
∴cn+1≤cn,
∴n=1时,cn取到最大值
| 4 |
| 3 |
∵cn+m≤0对任意的n∈N+恒成立,
∴
| 4 |
| 3 |
∴m≤-
| 4 |
| 3 |
点评:本题主要考查了等差数列、等比数列的通项公式,考查恒成立问题,考查学生的计算能力,属于中档题.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
已知向量
=(1,2-x),
=(2+x,3),则向量
与
共线的一个充分不必要条件是( )
| a |
| b |
| a |
| b |
| A、x=±1 | ||||
| B、x=±1或0 | ||||
C、|
| ||||
D、
|

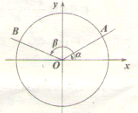 如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=
如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=