题目内容
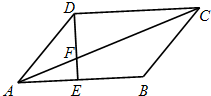如图，平行四边形ABCD中，AE：EB=1：2，若△AEF的面积等于1cm2 则△CDF的面积等于考点：相似三角形的性质,三角形的面积公式
专题：计算题,立体几何
分析：根据平行四边形对边平行，得到两个三角形相似，根据两个三角形相似，知道这两个三角形的面积之比等于边长之比的平方，做出两个三角形的边长之比，根据△AEF的面积等于1cm2，得到要求的三角形的面积．
解答：
解：平行四边形ABCD中，
有△AEF～△CDF
∴△AEF与△CDF的面积之比等于对应边长之比的平方，
∵AE：EB=1：2，
∴AE：CD=1：3
∵△AEF的面积等于1cm2，
∴△CDF的面积等于9cm2
故答案为：9
有△AEF～△CDF
∴△AEF与△CDF的面积之比等于对应边长之比的平方，
∵AE：EB=1：2，
∴AE：CD=1：3
∵△AEF的面积等于1cm2，
∴△CDF的面积等于9cm2
故答案为：9
点评：本题考查三角形相似的性质，两个三角形相似，对应的高线，中线和角平分线之比等于边长之比，两个三角形的面积之比等于边长比的平方，这种性质用的比较多．
练习册系列答案
名校课堂系列答案
相关题目
已知命题p：?x∈R，cosx=
，命题q：?x∈R，x2-2x+2＞0，则下列判断正确的是（ ）
| 5 |
| 4 |
| A、p∨q为假 |
| B、p∧q为真 |
| C、￢p∨￢q为假 |
| D、￢p∧q为真 |
下列函数中，既是偶函数且值域为（-∞，0]的函数是（ ）
| A、f（x）=xsinx |
| B、f（x）=-2-x |
| C、f（x）=ln|x| |
| D、f（x）=-x2 |
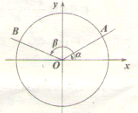如图所示，锐角α和钝角β的始边与x轴的非负半轴重合，终边分别与单位圆交于A、B两点，角α的终边与射线y=