题目内容
 已知a为执行如图所示的程序框图输出的结果,又在数列{an}中,a1=1,an+1=2an+a,则( )
已知a为执行如图所示的程序框图输出的结果,又在数列{an}中,a1=1,an+1=2an+a,则( )A、an=
| ||||
B、an=2n-2+
| ||||
| C、an=3•2n-1-2 | ||||
| D、an=-2n+3 |
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:根据框图的流程依次计算运行的结果,直到满足条件S≥2014,求得输出a的值,再利用等比数列的通项公式求解即可.
解答:
解:由程序框图知:程序第一次运行a=
=-3,i=1+1=2,;
第二次运行a=
=-
,i=2+1=3;
第三次运行a=
=
,i=3+1=4;
第四次运行a=
=2,i=4+1=5;
…,
最后一次得到a=2.
∴输出i=7,
∵an+1=2an+a,
∴an+1+2=2an+4,
∴an+1+2=2(an+2),
∴
=2,
∴数列{an+2}是一个首项为
3公比为2的等比数列,
∴数列an+2=3×2n-1,
∴an=3×2n-1-2,
故选:C.
| 1+2 |
| 1-2 |
第二次运行a=
| 1-3 |
| 1+3 |
| 1 |
| 2 |
第三次运行a=
1-
| ||
1+
|
| 1 |
| 3 |
第四次运行a=
1+
| ||
1-
|
…,
最后一次得到a=2.
∴输出i=7,
∵an+1=2an+a,
∴an+1+2=2an+4,
∴an+1+2=2(an+2),
∴
| an+1+2 |
| an+2 |
∴数列{an+2}是一个首项为
3公比为2的等比数列,
∴数列an+2=3×2n-1,
∴an=3×2n-1-2,
故选:C.
点评:本题考查了循环结构的程序框图,考查了数列的通项公式及其求解方法,根据框图的流程依次计算运行的结果是解答此类问题的常用方法.

练习册系列答案
相关题目
已知命题p:?x∈R,cosx=
,命题q:?x∈R,x2-2x+2>0,则下列判断正确的是( )
| 5 |
| 4 |
| A、p∨q为假 |
| B、p∧q为真 |
| C、¬p∨¬q为假 |
| D、¬p∧q为真 |
已知向量
=(1,2-x),
=(2+x,3),则向量
与
共线的一个充分不必要条件是( )
| a |
| b |
| a |
| b |
| A、x=±1 | ||||
| B、x=±1或0 | ||||
C、|
| ||||
D、
|
 一个算法的程序框图如图所示,若该程序输出的结果为12,则判断框中应填入的条件是( )
一个算法的程序框图如图所示,若该程序输出的结果为12,则判断框中应填入的条件是( )| A、k≤4 | B、k≤3 |
| C、k<3 | D、k≥3 |
函数f(x)=sin(ωx+
)(ω>0)的图象与x轴的交点的横坐标构成一个公差为
的等差数列,要得到函数g(x)=sinωx的图象,只需将f(x)的图象( )
| π |
| 6 |
| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
下列函数中,既是偶函数且值域为(-∞,0]的函数是( )
| A、f(x)=xsinx |
| B、f(x)=-2-x |
| C、f(x)=ln|x| |
| D、f(x)=-x2 |
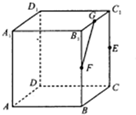 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是棱CC1、BB1、B1C1的中点,H是线段FG上一动点,则下列命题正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、G分别是棱CC1、BB1、B1C1的中点,H是线段FG上一动点,则下列命题正确的是