题目内容
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1、F2,P为双曲线上一点,且满足|OP|=$\sqrt{11}$a,|F1F2|是|PF1|与|PF2|的等比中项,则该双曲线的离心率为( )| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 通过等比数列双曲线的定义,余弦定理推出:|OP|2=2a2+3c2.利用|OP|=$\sqrt{11}$a,求出双曲线的离心率的值.
解答 解:由题意,|PF1|、|F1F2|、|PF2|成等比数列可知,|F1F2|2=|PF1||PF2|,
即4c2=|PF1||PF2|,
由双曲线的定义可知|PF1|-|PF2|=2a,即|PF1|2+|PF2|2-2|PF1||PF2|=4a2,
可得|PF1|2+|PF2|2-8c2=4a2…①
设∠POF1=θ,则∠POF2=π-θ,
由余弦定理可得:|PF2|2=c2+|OP|2-2|OF2||OP|cos(π-θ),|PF1|2=c2+|OP|2-2|OF1||OP|cosθ,
|PF2|2+PF1|2=2c2+2|OP|2,…②,
由①②化简得:|OP|2=2a2+3c2.
因为|OP|=$\sqrt{11}$a,所以2a2+3c2=11a2.
所以e=$\frac{c}{a}$=$\sqrt{3}$.
故选:D.
点评 本题考查双曲线的定义,余弦定理以及等比数列的应用,是有难度的综合问题,考查分析问题解决问题的能力.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
12.一个几何体的三视图如图所示,则该几何体的体积为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19.在图中,U表示全集,用A、B表出阴影部分,其中表示正确的是( )


| A. | A∪B | B. | A∩B | C. | ∁U(A∩B) | D. | (∁UA)∩B |
13.设正实数a,b满足a+λb=2(其中λ为正常数).若ab的最大值为3,则λ=( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
14.若二次函数f(x)=x2-2mx-5在区间(3,4)上存在一个零点,则m的取值范围是( )
| A. | $\frac{2}{3}<m<\frac{11}{8}$ | B. | $m<\frac{11}{8}$ | C. | $m>\frac{2}{3}$ | D. | $m<\frac{2}{3}$或$m>\frac{11}{8}$ |
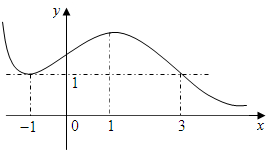 f′(x)为定义在R上的函数f(x)的导函数,而y=3f'(x)的图象如图所示,则y=f(x)的单调递增区间是(-∞,3].
f′(x)为定义在R上的函数f(x)的导函数,而y=3f'(x)的图象如图所示,则y=f(x)的单调递增区间是(-∞,3].