题目内容
15.直线$|\begin{array}{l}{x}&{y}\\{2}&{1}\end{array}|$=3的一个方向向量可以是(-2,-1)..分析 平面中,直线方程Ax+By+C=0它的一个方向向量是(B,-A),由此利用二阶行列式展开式能求出直线的一个方向向量.
解答 解:∵直线$|\begin{array}{l}{x}&{y}\\{2}&{1}\end{array}|$=3,
∴x-2y-3=0.
∴直线$|\begin{array}{l}{x}&{y}\\{2}&{1}\end{array}|$=3的一个方向向量可以是(-2,-1).
故答案为:(-2,-1).
点评 本题考查直线的方向向量的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
10.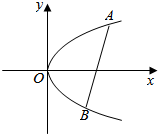 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )| A. | 2p | B. | $\frac{5}{2}p$ | C. | $\frac{3}{2}p$ | D. | 3p |
7.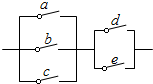 如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
 如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |