题目内容
16.若x,y满足不等式组$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$,则z=$\frac{1}{2}$x+y的最小值是$\frac{3}{2}$.分析 由约束条件作出可行域,化向量数量积为线性目标函数,数形结合得到最优解,求出最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$,作出可行域如图,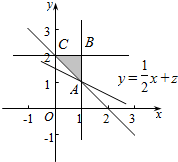
∵z=$\frac{1}{2}$x+y,化为y=-$\frac{1}{2}$x+z,
由图可知,当直线y=-$\frac{1}{2}$x+z过A(1,1)时,目标函数有最小值,
Zmin=$\frac{1}{2}$×1+1=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了简单的线性规划,考查了平面向量的数量积,训练了数形结合的解题思想方法,是中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
7.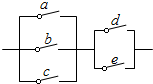 如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
 如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1、F2,P为双曲线上一点,且满足|OP|=$\sqrt{11}$a,|F1F2|是|PF1|与|PF2|的等比中项,则该双曲线的离心率为( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
11.有编号为A1,A2,…,A9的9道题,其难度系数如表:
其中难度系数小于0.50的为难题.
(Ⅰ)从上述9道题中,随机抽取1道,求这道题为难题的概率;
(Ⅱ)从难题中随机抽取2道,求这两道题目难度系数相等的概率.
| 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 |
| 难度系数 | 0.48 | 0.56 | 0.52 | 0.37 | 0.69 | 0.47 | 0.47 | 0.58 | 0.50 |
(Ⅰ)从上述9道题中,随机抽取1道,求这道题为难题的概率;
(Ⅱ)从难题中随机抽取2道,求这两道题目难度系数相等的概率.
1.函数f(x)=3${\;}^{\sqrt{x-2}}$的定义域为( )
| A. | (-∞,0) | B. | [0,+∞) | C. | [2,+∞) | D. | (-∞,2) |