题目内容
已知奇函数f(x)满足f(-1)=f(3)=0,在区间(-2,0)上是减函数,在区间(2,+∞)是增函数,函数F(x)=
,则{x|F(x)>0}=( )
|
| A、{x|x<-3,或0<x<2,或x>3} |
| B、{x|x<-3,或-1<x<0,或0<x<1,或x>3} |
| C、{x|-3<x<-1,或1<x<3} |
| D、{x|x<-3,或0<x<1,或1<x<2,或2<x<3} |
考点:分段函数的应用
专题:计算题,综合题,函数的性质及应用
分析:根据奇函数f(x)满足f(-1)=f(3)=0,在区间(-2,0)上是减函数,在区间(2,+∞)是增函数,可得-3<x<-1或0<x<1,或x>3时,f(x)>0;x<-3或-1<x<0或1<x<3时,f(x)<0,再将不等式等价变形,即可得到结论.
解答:
解:∵奇函数f(x)满足f(-1)=f(3)=0,
在区间(-2,0)上是减函数,在区间(2,+∞)是增函数,
∴-3<x<-1或0<x<1,或x>3时,f(x)>0;
x<-3或-1<x<0或1<x<3时,f(x)<0.
∵函数F(x)=
,
∴x>0且-f(x)>0,或x<0且xf(-x)>0时,F(x)>0,
∴x>0且f(x)<0,或x<0且f(x)>0时,F(x)>0,
∴-3<x<-1或1<x<3,
故选C.
在区间(-2,0)上是减函数,在区间(2,+∞)是增函数,
∴-3<x<-1或0<x<1,或x>3时,f(x)>0;
x<-3或-1<x<0或1<x<3时,f(x)<0.
∵函数F(x)=
|
∴x>0且-f(x)>0,或x<0且xf(-x)>0时,F(x)>0,
∴x>0且f(x)<0,或x<0且f(x)>0时,F(x)>0,
∴-3<x<-1或1<x<3,
故选C.
点评:本题考查函数单调性与奇偶性的结合,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=2x2-mx+5,m∈R,它在(-∞,-2]上单调递减,则f(1)的取值范围是( )
| A、f(1)=15 |
| B、f(1)>15 |
| C、f(1)≤15 |
| D、f(1)≥15 |
下列说法正确的是( )
| A、三点确定一个平面 |
| B、四边形一定是平面图形 |
| C、梯形一定是平面图形 |
| D、平面α和平面β有不同在一条直线上的三个公共点 |
一植物园参观路径如图所示,若要全部参观并且路线不重复,则不同的参观路线种数共有( )
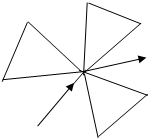

| A、6种 | B、8种 |
| C、36种 | D、48种 |