题目内容
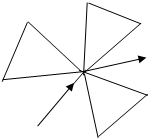
一植物园参观路径如图所示，若要全部参观并且路线不重复，则不同的参观路线种数共有（ ）
| A、6种 | B、8种 |
| C、36种 | D、48种 |
考点：排列、组合及简单计数问题
专题：排列组合
分析：站在中间，从三个区域任意选一个是3种，但是你是选择逆时针走还是顺时针走又有2种所以是2×3，完成了第一步．然后再从剩下的2个圈选择一个2×2，最后一个圈1×2，这个过程是分步的所以是相乘，则2×3×2×2×1×2=48
解答：
解：如图所示：
站在中间，从三个区域任意选一个是3种，但是你是选择逆时针走还是顺时针走又有2种所以是2×3，完成了第一步．
然后再从剩下的2个圈选择一个2×2，最后一个圈1×2，这个过程是分步的所以是相乘，则2×3×2×1×2=48
故选：D．
站在中间，从三个区域任意选一个是3种，但是你是选择逆时针走还是顺时针走又有2种所以是2×3，完成了第一步．
然后再从剩下的2个圈选择一个2×2，最后一个圈1×2，这个过程是分步的所以是相乘，则2×3×2×1×2=48
故选：D．
点评：本题主要考察排列组合问题，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
过双曲线
-
=1（a＞0，b＞0）的左焦点F1（-c，0）（c＞0）作圆x2+y2=
的切线，切点为E，直线F1E交双曲线右支于点P，若
=
（
+
），则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
| OE |
| 1 |
| 2 |
| OF1 |
| OP |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列{an}满足a1=1，且an=
an-1+（
）n（n≥2，且n∈N*），则{an}的通项公式为（ ）
| 1 |
| 3 |
| 1 |
| 3 |
A、
| ||
B、
| ||
| C、n+2 | ||
| D、（n+2）3n |
已知奇函数f（x）满足f（-1）=f（3）=0，在区间（-2，0）上是减函数，在区间（2，+∞）是增函数，函数F（x）=
，则{x|F（x）＞0}=（ ）
|
| A、{x|x＜-3，或0＜x＜2，或x＞3} |
| B、{x|x＜-3，或-1＜x＜0，或0＜x＜1，或x＞3} |
| C、{x|-3＜x＜-1，或1＜x＜3} |
| D、{x|x＜-3，或0＜x＜1，或1＜x＜2，或2＜x＜3} |