题目内容
已知f(x)=x3+ax2+bx+c,在x=1与x=-2时,都取得极值.
(Ⅰ)求a,b的值;
(Ⅱ)若x∈[-3,2]都有f(x)>
-
,(c>0)恒成立,求c的取值范围.
(Ⅰ)求a,b的值;
(Ⅱ)若x∈[-3,2]都有f(x)>
| 4 |
| c |
| 1 |
| 2 |
考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)求出f′(x)并令其=0得到方程,把x=-1和x=2代入求出a、b即可;
(2)求出函数的最小值为f(1),要使不等式恒成立,既要证f(1)>
-
,即可求出c的取值范围.
(2)求出函数的最小值为f(1),要使不等式恒成立,既要证f(1)>
| 4 |
| c |
| 1 |
| 2 |
解答:
解:(1)f′(x)=3x2+2ax+b,
由题意:
即
,
解得
;
(2)由(Ⅰ)知,f′(x)=3x2+3x-6,
令f′(x)<0,解得-2<x<1;
令f′(x)>0,解得x<-2或x>1,
∴(x)的减区间为(-2,1);增区间为(-∞,-2),(1,+∞).
∴x∈[-3,2]时,
∴当x=1时,f(x)取得最小值-
+c,
∴f(x)min=-
+c>
-
,
解得c>4.
由题意:
|
|
解得
|
(2)由(Ⅰ)知,f′(x)=3x2+3x-6,
令f′(x)<0,解得-2<x<1;
令f′(x)>0,解得x<-2或x>1,
∴(x)的减区间为(-2,1);增区间为(-∞,-2),(1,+∞).
∴x∈[-3,2]时,
∴当x=1时,f(x)取得最小值-
| 7 |
| 2 |
∴f(x)min=-
| 7 |
| 2 |
| 4 |
| c |
| 1 |
| 2 |
解得c>4.
点评:考查学生利用导数求函数极值的能力,利用导数研究函数单调性的能力,以及掌握不等式的证明方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知q是等比数列{an}的公比,则“q<1”是“数列{an}是递减数列”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
已知奇函数f(x)满足f(-1)=f(3)=0,在区间(-2,0)上是减函数,在区间(2,+∞)是增函数,函数F(x)=
,则{x|F(x)>0}=( )
|
| A、{x|x<-3,或0<x<2,或x>3} |
| B、{x|x<-3,或-1<x<0,或0<x<1,或x>3} |
| C、{x|-3<x<-1,或1<x<3} |
| D、{x|x<-3,或0<x<1,或1<x<2,或2<x<3} |
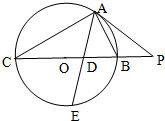 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10. ABC-A1B1C1是各棱长均相等的正三棱柱,D是侧棱CC1的中点.求证:平面AB1D⊥平面ABB1A1.
ABC-A1B1C1是各棱长均相等的正三棱柱,D是侧棱CC1的中点.求证:平面AB1D⊥平面ABB1A1.