题目内容
已知向量
和
的夹角为60°,|
|=10,|
|=8,求:
(1)|
+
|;
(2)
+
与
的夹角θ的余弦值.
| a |
| b |
| a |
| b |
(1)|
| a |
| b |
(2)
| a |
| b |
| a |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:(1)由模长公式可得|
+
|=
=
,代入已知数据计算可得;
(2)易求得(
+
)•
的值,代入夹角公式cosθ=
,计算可得.
| a |
| b |
(
|
|
(2)易求得(
| a |
| b |
| a |
(
| ||||||
|
|
解答:
解:(1)∵向量
和
的夹角为60°,|
|=10,|
|=8,
∴|
+
|=
=
=
=2
(2)∵(
+
)•
=
2+
•
=100+10×8×
=140,
∴cosθ=
=
=
| a |
| b |
| a |
| b |
∴|
| a |
| b |
(
|
|
=
102+2×10×8×
|
| 61 |
(2)∵(
| a |
| b |
| a |
| a |
| a |
| b |
| 1 |
| 2 |
∴cosθ=
(
| ||||||
|
|
| 140 | ||
2
|
7
| ||
| 61 |
点评:本题考查平面向量的数量积与夹角,涉及向量的模长公式,属基础题.

练习册系列答案
相关题目
已知奇函数f(x)满足f(-1)=f(3)=0,在区间(-2,0)上是减函数,在区间(2,+∞)是增函数,函数F(x)=
,则{x|F(x)>0}=( )
|
| A、{x|x<-3,或0<x<2,或x>3} |
| B、{x|x<-3,或-1<x<0,或0<x<1,或x>3} |
| C、{x|-3<x<-1,或1<x<3} |
| D、{x|x<-3,或0<x<1,或1<x<2,或2<x<3} |
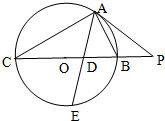 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10. ABC-A1B1C1是各棱长均相等的正三棱柱,D是侧棱CC1的中点.求证:平面AB1D⊥平面ABB1A1.
ABC-A1B1C1是各棱长均相等的正三棱柱,D是侧棱CC1的中点.求证:平面AB1D⊥平面ABB1A1.