题目内容
已知函数f（x）=sin（ωx+
）（ω＞0）在区间[-
，
]的端点上恰取相邻一个最大值点和一个最小值点，则
（1）ω的值为 ；
（2）在x=-
，x=
，y=1和x轴围成的矩形区域里掷一小球，小球恰好落在函数f（x）=sin（ωx+
）（x∈[-
，
]）与x轴围成的区域内的概率为 ．
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
（1）ω的值为
（2）在x=-
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,几何概型
专题：三角函数的图像与性质,概率与统计
分析：（1）依题意，可知
=π，从而可求得ω的值；
（2）易求
sin（x+
）dx=1，利用几何概型即可求得小球恰好落在函数f（x）=sin（ωx+
）（x∈[-
，
]）与x轴围成的区域内的概率．
| T |
| 2 |
（2）易求
| ∫ |
-
|
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
解答：
解：（1）∵函数f（x）=sin（ωx+
）（ω＞0）在区间[-
，
]的端点上恰取相邻一个最大值点和一个最小值点，
∴
=
-（
）=π，
∴T=
=2π，
∴ω=1；
（2）依题意，作图如下：矩形ABCD的面积S=[
-（-
）]×1=
，
又
sin（x+
）dx=-cos（x+
）
=-（0-1）=1，
∴小球恰好落在函数f（x）=sin（ωx+
）（x∈[-
，
]）与x轴围成的区域内的概率p=
=
；
故答案为：1；
．
解：（1）∵函数f（x）=sin（ωx+| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
∴
| T |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
∴T=
| 2π |
| ω |
∴ω=1；
（2）依题意，作图如下：矩形ABCD的面积S=[
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
又
| ∫ |
-
|
| π |
| 3 |
| π |
| 3 |
| | |
-
|
∴小球恰好落在函数f（x）=sin（ωx+
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| 1 | ||
|
| 2 |
| π |
故答案为：1；
| 2 |
| π |
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，着重考查几何概型，求得
sin（x+
）dx=1是关键，考查运算求解能力，属于中档题．
| ∫ |
-
|
| π |
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
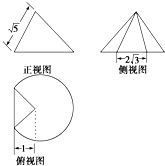一个圆锥被过其顶点的一个平面截去了较少的一部分几何体，余下的几何体的三视图如图，则余下部分的几何体的体积为（ ）A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如图所示是函数y=f（x）的图象，则函数y=f（x）的导函数图象是（ ）
A、 |
B、 |
C、 |
D、 |