题目内容
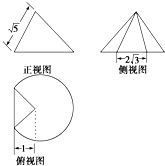 一个圆锥被过其顶点的一个平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )
一个圆锥被过其顶点的一个平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图求出圆锥母线,高,底面半径.进而求出锥体的底面积,代入锥体体积公式,可得答案.
解答:
解:由已知中的三视图,圆锥母线l=
=2
,圆锥的高h=
=2,
圆锥底面半径为r=
=2,
截去的底面弧的圆心角为120°,截去的面积是底面圆面积的
,
底面剩余部分为S=
πr2+
r2sin120°=
π+
,
故几何体的体积为:V=
Sh=
×(
π+
)×2=
+
,
故选:B
|
| 2 |
|
圆锥底面半径为r=
| l2-h2 |
截去的底面弧的圆心角为120°,截去的面积是底面圆面积的
| 2 |
| 3 |
底面剩余部分为S=
| 2 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
| 3 |
故几何体的体积为:V=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
| 3 |
| 16π |
| 9 |
2
| ||
| 3 |
故选:B
点评:本题考查几何体体积计算.本题关键是弄清几何体的结构特征,是易错之处.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
下面的程序框图,输出的结果为( )


| A、1 | B、2 | C、4 | D、16 |
复平面内,复数z=
,则复数z的共轭复数
对应的点的象限是( )
| 2+i |
| i2013 |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
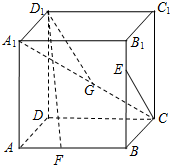 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论: