题目内容
求函数:y=
,x∈(-∞,0)∪(0,
]的值域.
| 4x2+2x+1 |
| x2 |
| 1 |
| 2 |
考点:函数的值域
专题:计算题,函数的性质及应用
分析:将原函数配方,令t=
,则由x<0或0<x<
,得t<0或t>2,y=(t+1)2+3,运用二次函数的图象和性质,即可得到值域.
| 1 |
| x |
| 1 |
| 2 |
解答:
解:y=
=4+
+(
)2
=(
+1)2+3,
令t=
,则由x<0或0<x<
,得t<0或t>2,
y=(t+1)2+3的对称轴t=-1,则y在t<0上递减,在t>2上递增,
则有y>4或y>12,
则函数的值域为(4,+∞).
| 4x2+2x+1 |
| x2 |
| 2 |
| x |
| 1 |
| x |
=(
| 1 |
| x |
令t=
| 1 |
| x |
| 1 |
| 2 |
y=(t+1)2+3的对称轴t=-1,则y在t<0上递减,在t>2上递增,
则有y>4或y>12,
则函数的值域为(4,+∞).
点评:本题考查函数的值域,考查可转化为二次函数的值域,注意对称轴和区间的关系,运用单调性解决,属于中档题.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
等差数列{an}前n项和Sn,满足S20=S40,下列结论正确的是( )
| A、S30是Sn中的最大值 |
| B、S20是Sn中的最小值 |
| C、S30=0 |
| D、S60=0 |
不等式组
所表示的平面区域的面积为( )
|
A、
| ||
| B、27 | ||
| C、30 | ||
D、
|
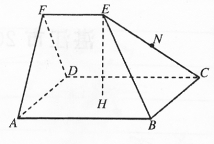 如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.
如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.