题目内容
 已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点
已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点(
| 2 |
| 3 |
(1)求双曲线C的方程;
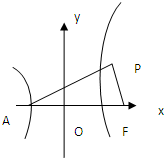
(2)若双曲线C的实轴左顶点为A,右焦点为F,在第一 象限任取双曲线C上的一点P,试问是否存在常数 λ(λ≠0),使∠PFA=λ∠PAF?
考点:双曲线的简单性质,双曲线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)先求抛物线的焦点为F(2,0),从而设双曲线方程,再将点(
,
)代入,可求双曲线C的方程;
(2)先假设成立,由当PF⊥x轴时,猜想结论λ=2;以此作为条件,再进行一般性探求与证明,证明当PF与x轴不垂直时∠PFA=2∠PAF成立.
| 2 |
| 3 |
(2)先假设成立,由当PF⊥x轴时,猜想结论λ=2;以此作为条件,再进行一般性探求与证明,证明当PF与x轴不垂直时∠PFA=2∠PAF成立.
解答:
解:(1)抛物线焦点为F(2,0),设双曲线方程为
-
=1,将点(
,
)代入得b2=3,
所以双曲线方程为x2-
=1.
(2)当PF⊥x轴时,P(2,3),|AF|=1+2=3,∴∠PFA=90°,∠PAF=45°,此时λ=2.
以下证明当PF与x轴不垂直时∠PFA=2∠PAF成立.
设P(x0,y0),则kPA=tan∠PAF=
,kPF=-tan∠PFA=
.
tan2∠PAF=
.
y02=3(x02-1)代入上式,得tan2∠PAF=-
=tan∠PFA恒成立,
∴∠PFA=2∠PAF恒成立.
| x2 |
| 4-b2 |
| y2 |
| b2 |
| 2 |
| 3 |
所以双曲线方程为x2-
| y2 |
| 3 |
(2)当PF⊥x轴时,P(2,3),|AF|=1+2=3,∴∠PFA=90°,∠PAF=45°,此时λ=2.
以下证明当PF与x轴不垂直时∠PFA=2∠PAF成立.
设P(x0,y0),则kPA=tan∠PAF=
| y0 |
| x0+1 |
| y0 |
| x0-2 |
tan2∠PAF=
| 2(x0+1)y0 |
| (x0+1)2-y02 |
y02=3(x02-1)代入上式,得tan2∠PAF=-
| y0 |
| x0-2 |
∴∠PFA=2∠PAF恒成立.
点评:本题考查利用待定系数法求双曲线的标准方程,考查存在性问题,通过假设存在,转化为封闭型命题进行求解.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
设
•
不共线,则下列四组向量中不能作为基底的是( )
| e1 |
| e2 |
A、
| ||||||||
B、3
| ||||||||
C、
| ||||||||
D、
|
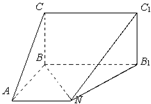 如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,
如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,