题目内容
设x,y满足约束条件
,若目标函数z=ax+2by(a>0,b>0)的最大值为1,则
+
的最小值为 .
|
| 1 |
| a2 |
| 1 |
| 4b2 |
考点:简单线性规划
专题:数形结合
分析:由约束条件作出可行域,化目标函数为直线方程斜截式,数形结合得到最优解,求出最优解的坐标,代入目标函数得到a,b的关系式,然后利用基本不等式求
+
的最小值.
| 1 |
| a2 |
| 1 |
| 4b2 |
解答:
解:由约束条件作可行域如图.

由图可知,使目标函数数z=ax+2by(a>0,b>0)取得最大值的点为B(1,1),
∴a+2b=1,
则
+
≥2
=
(当且仅当a=2b时取等号),
由
,解得:
.
∴
+
的最小值为
=
=8.
故答案为:8.

由图可知,使目标函数数z=ax+2by(a>0,b>0)取得最大值的点为B(1,1),
∴a+2b=1,
则
| 1 |
| a2 |
| 1 |
| 4b2 |
|
| 1 |
| ab |
由
|
|
∴
| 1 |
| a2 |
| 1 |
| 4b2 |
| 1 |
| ab |
| 1 | ||||
|
故答案为:8.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,训练了利用基本不等式求最值,是中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
函数y=sin|x|的图象是( )
A、 |
B、 |
C、 |
D、 |
向边长为2米的正方形木框ABCD内随机投掷一粒绿豆,记绿豆落点为P,则P点与A点的距离大于1米,同时使cos∠DPC∈(0,1)的概率为( )
A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
已知数列{an}的首项为a1=1,且满足对任意的n∈N*,都有an+1-an≤2n,an+2-an≥3×2n成立,则a2014=( )
| A、22014-1 |
| B、22014+1 |
| C、22015-1 |
| D、22015+1 |
已知
=(sinx,1,cox),
=(-1,sinx,cox)则
+
与
-
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
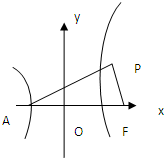 已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点
已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点