题目内容
在直角坐标系xOy中,曲线C的参数方程为
(θ为参数),若以直角坐标系xOy的O点为极点,x轴正方向为极轴,且长度单位相同,建立极坐标系,得直线l的极坐标方程为2ρcos(θ+
)=1.求直线l与曲线C交点的极坐标.
|
| π |
| 6 |
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:首先把直线l的极坐标方程2ρcos(θ+
)=1转化为直角坐标方程为:y=
x-1,然后曲线C的参数方程
(θ为参数),转化为普通方程x2=y+1(-
≤x≤
),建立方程组,解得结果再把直角坐标转化为极坐标.
| π |
| 6 |
| 3 |
|
| 2 |
| 2 |
解答:
解:直线l的极坐标方程2ρcos(θ+
)=1
转化为直角坐标方程为:y=
x-1,故直线l的倾斜角为
.
曲线C的参数方程
(θ为参数),转化为普通方程x2=y+1(-
≤x≤
),
由
解得
.
所以交点的极坐标为(1,-
).
故答案为:(1,-
)
| π |
| 6 |
转化为直角坐标方程为:y=
| 3 |
| π |
| 3 |
曲线C的参数方程
|
| 2 |
| 2 |
由
|
解得
|
所以交点的极坐标为(1,-
| π |
| 2 |
故答案为:(1,-
| π |
| 2 |
点评:本题考查的知识点:极坐标方程和直角坐标方程的互化,三角恒等式的应用,解方程组,极坐标和直角坐标的互化.

练习册系列答案
相关题目
P是△ABC所在平面内一点,
=λ
+
,则P点一定在( )
| CB |
| PA |
| PB |
| A、△ABC内部 |
| B、在直线AC上 |
| C、在直线AB上 |
| D、在直线BC上 |
实数的乘法运算与向量的数量积运算类比,不成立的运算律是( )
A、a×b=b×a类比
| ||||||||||||||
B、a×(b×c)=(a×b)×c类比
| ||||||||||||||
C、a2=|a|2类比
| ||||||||||||||
D、a(b+c)=ab+ac类比
|
 已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点
已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点

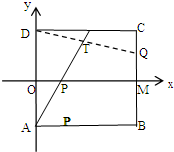 如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为
如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为