题目内容
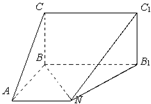 如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,
如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,且AB⊥BB1,BC=AB=AN=
| 1 |
| 2 |
(1)求证:BN⊥平面C1B1N;
(2)求此五面体的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)利用直线与平面垂直的性质定理证明B1C1⊥BN,然后利用勾股定理证明BN⊥B1N,通过B1N∩B1C1=B1,利用直线与平面垂直的判定定理证明:BN⊥平面C1B1N;
(2)连接CN,说明NM⊥平面B1C1CB,然后五面体的体积V=VC-ABN+VN-B1C1CB分别求解即可.
(2)连接CN,说明NM⊥平面B1C1CB,然后五面体的体积V=VC-ABN+VN-B1C1CB分别求解即可.
解答:
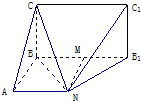 解:(1)证明:连4,过N作NM⊥BB1,垂足为M,
解:(1)证明:连4,过N作NM⊥BB1,垂足为M,
∵B1C1⊥平面ABB1N,BN?平面ABB1N,
∴B1C1⊥BN,…(2分)
又,BC=4,AB=4,BM=AN=4,BA⊥AN,
∴BN=
=4
,B1N=
=
=4
,
∵BB1=82=64,B1N2+BN2=32+32=64,
∴BN⊥B1N,…(4分)
∵B1C1?平面B1C1N,B1N?平面B1C1N,B1N∩B1C1=B1
∴BN⊥平面C1B1N…(6分)
(2)连接CN,VC-ABN=
×BC•S△ABN=
×4×
×4×4=
,…(8分)
又B1C1⊥平面ABB1N,所以平面CBB1C1⊥平面ABB1N,且平面CBB1C1∩ABB1N=BB1,NM⊥BB1,
NM?平面B1C1CB,
∴NM⊥平面B1C1CB,…(9分)
VN-B1C1CB=
×NM•S矩形B1C1CB=
×4×4×8=
…(11分)
此几何体的体积V=VC-ABN+VN-B1C1CB=
+
=
…(12分)
 解:(1)证明:连4,过N作NM⊥BB1,垂足为M,
解:(1)证明:连4,过N作NM⊥BB1,垂足为M,∵B1C1⊥平面ABB1N,BN?平面ABB1N,
∴B1C1⊥BN,…(2分)
又,BC=4,AB=4,BM=AN=4,BA⊥AN,
∴BN=
| 42+42 |
| 2 |
| NM2+B1M2 |
| 42+42 |
| 2 |
∵BB1=82=64,B1N2+BN2=32+32=64,
∴BN⊥B1N,…(4分)
∵B1C1?平面B1C1N,B1N?平面B1C1N,B1N∩B1C1=B1
∴BN⊥平面C1B1N…(6分)
(2)连接CN,VC-ABN=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 32 |
| 3 |
又B1C1⊥平面ABB1N,所以平面CBB1C1⊥平面ABB1N,且平面CBB1C1∩ABB1N=BB1,NM⊥BB1,
NM?平面B1C1CB,
∴NM⊥平面B1C1CB,…(9分)
VN-B1C1CB=
| 1 |
| 3 |
| 1 |
| 3 |
| 128 |
| 3 |
此几何体的体积V=VC-ABN+VN-B1C1CB=
| 32 |
| 3 |
| 128 |
| 3 |
| 160 |
| 3 |
点评:本题考查直线与平面垂直的判定定理以及性质定理的应用,几何体的体积的求法,考查转化思想以及空间想象能力.

练习册系列答案
相关题目
函数f(x)=x-lnx的单调递减区间为( )
| A、(-∞,1) |
| B、(1,+∞) |
| C、(0,1) |
| D、(0,+∞) |
下列命题中:
①若
•
=0,则
=
或
=
;
②若不平行的两个非零向量
,
满足|
|=|
|,则(
+
)•(
-
)=0;
③若
与
平行,则|
•
|=|
|•|
|;
④若
∥
,
∥
,则
∥
;
其中假命题的个数是( )
①若
| a |
| b |
| a |
| 0 |
| b |
| 0 |
②若不平行的两个非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
③若
| a |
| b |
| a |
| b |
| a |
| b |
④若
| a |
| b |
| b |
| c |
| a |
| c |
其中假命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
函数f(x)的图象如图所示,下列数值排序正确的是( )
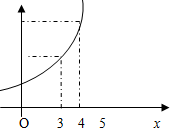

| A、0<f′(3)<f′(4)<f(4)-f(3) |
| B、0<f′(3)<f(4)-f(3)<f′(4) |
| C、0<f′(4)<f′(3)<f(4)-f(3) |
| D、0<f(4)-f(3)<f′(3)<f′(4) |
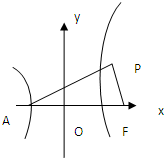 已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点
已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点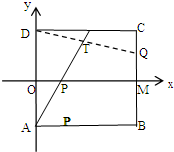 如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为
如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为