题目内容
求函数y=3sin(2x+
)+1的周期、单调区间及最大、最小值.
| π |
| 6 |
考点:复合三角函数的单调性
专题:三角函数的图像与性质
分析:直接由周期公式求周期,利用复合函数的单调性求单调期间,同时求得使函数取得最值的x的集合.
解答:
解:∵函数y=3sin(2x+
)+1,
∴T=
=π.
由-
+2kπ≤2x+
≤
+2kπ,得-
+kπ≤x≤
+kπ,k∈Z.
∴函数y=3sin(2x+
)+1的单调增区间为[-
+kπ,
+kπ],k∈Z.
由
+2kπ≤2x+
≤
+2kπ,得
+kπ≤x≤
+kπ,k∈Z.
∴函数y=3sin(2x+
)+1的单调减区间为[
+kπ,
+kπ],k∈Z.
函数的最大值为4,取得最大值的x的集合为:{x|x=
+kπ,k∈Z}.
函数的最小值为-2,取得最小值的x的集合为:{x|x=
+kπ,k∈Z}.
| π |
| 6 |
∴T=
| 2π |
| 2 |
由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴函数y=3sin(2x+
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
∴函数y=3sin(2x+
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
函数的最大值为4,取得最大值的x的集合为:{x|x=
| π |
| 6 |
函数的最小值为-2,取得最小值的x的集合为:{x|x=
| 2π |
| 3 |
点评:本题考查了y=Asin(ωx+φ)+k型函数的图象和性质,关键是熟记教材基础知识,是基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
“m=-1”是“直线mx+(2m-1)y+1=0和直线3x+my+2=0垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
实数的乘法运算与向量的数量积运算类比,不成立的运算律是( )
A、a×b=b×a类比
| ||||||||||||||
B、a×(b×c)=(a×b)×c类比
| ||||||||||||||
C、a2=|a|2类比
| ||||||||||||||
D、a(b+c)=ab+ac类比
|
函数f(x)=x-lnx的单调递减区间为( )
| A、(-∞,1) |
| B、(1,+∞) |
| C、(0,1) |
| D、(0,+∞) |
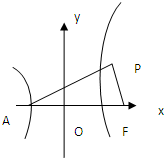 已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点
已知双曲线C的中心在原点,抛物线y2=8x的焦点是双曲线的一个焦点,且C过点