题目内容
“幸福感指数”是指某个人主观的评价他对自己目前生活状态的满意程度时给出的区间[0，10]内的一个数，该数越接近10表示越满意．为了解某大城市市民的幸福感，随时对该城市的男、女市民各500人进行了调查．调查数据如下表所示．
如果市民幸福感指数达到6，则认为该市民幸福．根据表格，解答下面的问题：
（I）完成下列2×2列联表
（II）试在犯错误概率不超过0.01的前提下能否判定该市市民幸福与否与性别有关？
参考公式：k2=
| 幸福感指数 | [0，2） | [2，4） | [4，6） | [6，8） | [8，10） |
| 男市民人数 | 10 | 20 | 220 | 125 | 125 |
| 女市民人数 | 10 | 10 | 180 | 175 | 125 |
（I）完成下列2×2列联表
参考公式：k2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P（k2≥k0） | 0.10 | 0.01 | 0.001 |
| k0 | 2.706 | 6.635 | 10.828 |
考点：独立性检验
专题：计算题,概率与统计
分析：（Ⅰ）由题意中的数据填入列联表即可；
（Ⅱ）利用公式k2=
求出其值，查下表即可．
（Ⅱ）利用公式k2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
解答：
解：（Ⅰ）列联表如下：
（Ⅱ）k2=
=
≈10.101＞6.635，
又∵P（k2≥6.635）=0.01；
故在犯错误概率不超过0.01的前提下能认为该市市民幸福与性别有关．
| 不幸福 | 幸福 | 合计 | |
| 男市民人数 | 250 | 250 | 500 |
| 女市民人数 | 200 | 300 | 500 |
| 合计 | 450 | 550 | 1000 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 1000×(250×300-250×200)2 |
| 450×550×500×500 |
又∵P（k2≥6.635）=0.01；
故在犯错误概率不超过0.01的前提下能认为该市市民幸福与性别有关．
点评：本题考查了列联表的填写方法及独立性检验的做法，属于基础题．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
向边长为2米的正方形木框ABCD内随机投掷一粒绿豆，记绿豆落点为P，则P点与A点的距离大于1米，同时使cos∠DPC∈（0，1）的概率为（ ）
A、1-
| ||
B、1-
| ||
C、
| ||
D、
|
已知椭圆
+y2=1和双曲线
-y2=1共焦点F1，F2，P为两曲线的一个公共点，则∠F1PF2的大小为（ ）
| x |
| m |
| x2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
P是△ABC所在平面内一点，
=λ
+
，则P点一定在（ ）
| CB |
| PA |
| PB |
| A、△ABC内部 |
| B、在直线AC上 |
| C、在直线AB上 |
| D、在直线BC上 |
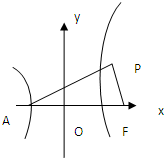已知双曲线C的中心在原点，抛物线y2=8x的焦点是双曲线的一个焦点，且C过点