题目内容

设
e1
•
e2
不共线，则下列四组向量中不能作为基底的是（　　）
A、
e1
+
e2
与
e1
-
e2
B、3
e1
-2
e2
与4
e2
-6
e1
C、
e1
+2
e2
与
e2
+2
e1
D、
e2
和
e1
+
e2
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由共线的向量不能作为平面向量的一组基底，能求出结果．
解答： 解：在A中，∵
e1
，
e2
不共线是两不共线的向量，
∴
e1
+
e2
与
e1
-
e2
不共线，
∴
e1
+
e2
与
e1
-
e2
能作为平面向量的一组基底．
在B中．，∵
e1
，
e2
不是两不共线的向量，
∴3
e1
-2
e2
=
1
2
（4
e1
-6
e2
）共线，
∴3
e1
-2
e2
与4
e1
-6
e2
不能作为平面向量的一组基底
在C中，∵
e1
，
e2
不是两不共线的向量，
∴
e1
+2
e2
与2
e1
+
e2
不共线，
∴
e1
+2
e2
与2
e1
+
e2
能作为平面向量的一组基底，
在D中，∵
e1
，
e2
是两不共线的向量，
∴
e2
和
e1
+
e2
不共线，
∴
e2
和
e1
+
e2
能作为平面向量的一组基底．
故选B．
点评：本题考查平行向量的性质和应用，是基础题．解题时要认真审题，正确解题的关键是知道共线的向量不能作为平面向量的一组基底．
练习册系列答案
相关题目
函数y=sin|x|的图象是（　　）
A、
B、
C、
D、
已知
a
=（sinx，1，cox），
b
=（-1，sinx，cox）则
a
+
b
与
a
-
b
的夹角为（　　）
A、
π
6
B、
π
4
C、
π
3
D、
π
2
用数学归纳法证明
1
22
+
1
32
+…+
1
(n+1)2
＞
1
2
-
1
n+2
，假设n=k时，不等式成立，则当n=k+1时，应推证的目标不等式是
 
．
若|
a
|=|
b
|=|
a
•
b
|，则
b
与
a
+
b
的夹角为（　　）
A、30°B、60°
C、150°D、120°
若向量
a
与
b
不共线，
a
•
b
≠0，且
c
=
a
-（
a
•
a
a
•
b
）
b
，则
a
与
c
的夹角为
 
．
已知椭圆
x
m
+y2=1和双曲线
x2
n2
-y2=1共焦点F1，F2，P为两曲线的一个公共点，则∠F1PF2的大小为（　　）
A、
π
3
B、
π
4
C、
2
3
π
D、
π
2
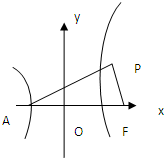已知双曲线C的中心在原点，抛物线y2=8x的焦点是双曲线的一个焦点，且C过点
（
2
，
3
）
（1）求双曲线C的方程；
（2）若双曲线C的实轴左顶点为A，右焦点为F，在第一 象限任取双曲线C上的一点P，试问是否存在常数 λ（λ≠0），使∠PFA=λ∠PAF？
函数f（x）=x-lnx的单调递减区间为（　　）
A、（-∞，1）
B、（1，+∞）
C、（0，1）
D、（0，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网