题目内容
已知椭圆中心在原点,焦点在x轴上,椭圆短轴的端点和焦点组成的四边形为正方形,且
=4.
(1)求椭圆方程;
(2)直线l过点P(0,2),且与椭圆相交于A、B两点,当△AOB面积取得最大值时,求直线l的方程.
| 2a2 |
| c |
(1)求椭圆方程;
(2)直线l过点P(0,2),且与椭圆相交于A、B两点,当△AOB面积取得最大值时,求直线l的方程.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(1)设椭圆方程为
+
=1(a>b>0).由条件得b=c,a2=2c,a2=b2+c2,解出即可;
(2)直线l的斜率一定存在,设直线l的方程为:y=kx+2,联立直线和椭圆方程,消去y得关于x的方程,运用韦达定理,弦长公式以及三角形的面积公式,再由基本不等式即可得到最大值.
| x2 |
| a2 |
| y2 |
| b2 |
(2)直线l的斜率一定存在,设直线l的方程为:y=kx+2,联立直线和椭圆方程,消去y得关于x的方程,运用韦达定理,弦长公式以及三角形的面积公式,再由基本不等式即可得到最大值.
解答:
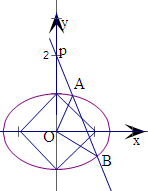 解:(1)设椭圆方程为
解:(1)设椭圆方程为
+
=1(a>b>0).
则由条件得,b=c,a2=2c,a2=b2+c2,
解得a2=2,b=c=1.
故椭圆方程为
+y2=1
(2)直线l的斜率一定存在,设直线l的方程为:y=kx+2,
由y=kx+2和椭圆方程
+y2=1,联立,消去y得
(1+2k2)x2+8kx+6=0,
设A(x1,y1),B(x2,y2),则x1+x2=-
,x1x2=
,
∵△>0,∴k2>
,
∴|AB|=
,
又O到直线AB的距离为d=
,
∴S△AOB=
|AB|d=
=2
•
令t=
(t>0),则S=2
•
≤
,
当且仅当t2=4,即k=±
时,取等号,
此时直线方程为y=±
x+2.
 解:(1)设椭圆方程为
解:(1)设椭圆方程为| x2 |
| a2 |
| y2 |
| b2 |
则由条件得,b=c,a2=2c,a2=b2+c2,
解得a2=2,b=c=1.
故椭圆方程为
| x2 |
| 2 |
(2)直线l的斜率一定存在,设直线l的方程为:y=kx+2,
由y=kx+2和椭圆方程
| x2 |
| 2 |
(1+2k2)x2+8kx+6=0,
设A(x1,y1),B(x2,y2),则x1+x2=-
| 8kx |
| 1+2k2 |
| 6 |
| 1+2k2 |
∵△>0,∴k2>
| 3 |
| 2 |
∴|AB|=
(1+k2)[
|
又O到直线AB的距离为d=
| 2 | ||
|
∴S△AOB=
| 1 |
| 2 |
| ||
| 1+2k2 |
| 2 |
| ||
| 1+2k2 |
令t=
| 2k2-3 |
| 2 |
| 1 | ||
t+
|
| ||
| 2 |
当且仅当t2=4,即k=±
| ||
| 2 |
此时直线方程为y=±
| ||
| 2 |
点评:本题考查椭圆的方程和性质及运用,考查直线和椭圆方程联立,消去一个未知数,运用韦达定理,和弦长公式,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
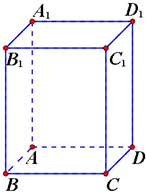 长方体ABCD-A1B1C1D1中,宽、长、高分别为3、4、5,现有一个小虫从A出发沿长方体表面爬行到C1来获取食物,求其路程的最小值.
长方体ABCD-A1B1C1D1中,宽、长、高分别为3、4、5,现有一个小虫从A出发沿长方体表面爬行到C1来获取食物,求其路程的最小值.