题目内容
求函数y=3+2sin(
-2x),x∈(0,π)的单调增区间.
| π |
| 3 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由诱导公式将函数的解析式化为:y=3+2sin(2x+
),令 2kπ-
≤2x+
≤2kπ+
,k∈z,结合x∈(0,π)求出x的范围,可得答案.
| 2π |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
解答:
解:函数y=3+2sin(
-2x)=3+2sin[π-(
-2x)]=3+2sin(2x+
),
令 2kπ-
≤2x+
≤2kπ+
,k∈z,
解得:kπ-
≤x≤kπ-
,k∈z,
又∵x∈(0,π),
∴函数y=3+2sin(
-2x),x∈(0,π)的单调增区间为:[
π,
π](k∈z)
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
令 2kπ-
| π |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
解得:kπ-
| 7π |
| 12 |
| π |
| 12 |
又∵x∈(0,π),
∴函数y=3+2sin(
| π |
| 3 |
| 5 |
| 12 |
| 11 |
| 12 |
点评:本题主要考查复合三角函数的单调性,熟练掌握正弦型函数的图象和性质是解答的关键,属于中档题.

练习册系列答案
相关题目
若f(x)是(-a,a)上的可导奇函数,且f'(x)不恒为零,则f'(x)在(-a,a)上( )
| A、必为奇函数 |
| B、必为偶函数 |
| C、是非奇非偶函数 |
| D、可能为奇函数,也可能是偶函数 |
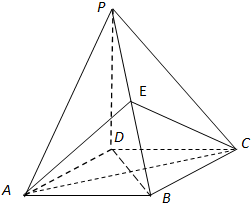 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.