题目内容
已知数列{an}中,a1=a,an+1=c-
.
(Ⅰ)设a=c=2,bn=
,求数列{bn}的通项公式;
(Ⅱ)设a=1,求证:{an}是递增数列的充分必要条件是c>2.
| 1 |
| an |
(Ⅰ)设a=c=2,bn=
| 1 |
| an-1 |
(Ⅱ)设a=1,求证:{an}是递增数列的充分必要条件是c>2.
考点:必要条件、充分条件与充要条件的判断,数列递推式
专题:计算题,等差数列与等比数列,简易逻辑
分析:(Ⅰ)代入向bn化简,可证明为等差数列;(Ⅱ)要分开证明必要性与充分性.
解答:
解:(Ⅰ)∵a=c=2,
∴an+1-1=1-
=
;
∴
=
+1,
即:bn+1-bn=1,
∴数列{bn}是公差为1的等差数列,
又b1=1,
∴bn=n.
(Ⅱ)证明:“必要性”
∵数列{an}递增,
∴a2>a1,
∵a1=1,a2=c-1,∴c-1>1,
∴c>2.
“充分性”
①n=1时,显然成立;
②假设ak+1>ak>0(k≥1,k∈N)成立,则
<
,
那么ak+2=c-
>c-
=ak+1
综合①②得an+1>an>0(n∈N*)成立.
即c>2时,数列{an}递增,
综上所述,{an}是递增数列的充分必要条件是c>2.
∴an+1-1=1-
| 1 |
| an |
| an-1 |
| an |
∴
| 1 |
| an+1-1 |
| 1 |
| an-1 |
即:bn+1-bn=1,
∴数列{bn}是公差为1的等差数列,
又b1=1,
∴bn=n.
(Ⅱ)证明:“必要性”
∵数列{an}递增,
∴a2>a1,
∵a1=1,a2=c-1,∴c-1>1,
∴c>2.
“充分性”
①n=1时,显然成立;
②假设ak+1>ak>0(k≥1,k∈N)成立,则
| 1 |
| ak+1 |
| 1 |
| ak |
那么ak+2=c-
| 1 |
| ak+1 |
| 1 |
| ak |
综合①②得an+1>an>0(n∈N*)成立.
即c>2时,数列{an}递增,
综上所述,{an}是递增数列的充分必要条件是c>2.
点评:本题考查了等差等比数列,同时考查了数学归纳法,属于中档题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
在R上可导的函数f(x)的图形如图所示,则关于x的不等式x•f′(x)<0的解集为( )
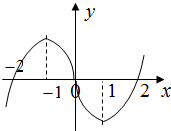
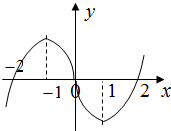
| A、(-∞,-1)∪(0,1) |
| B、(-1,0)∪(1,+∞) |
| C、(-2,-1)∪(1,2) |
| D、(-∞,-2)∪(2,+∞) |
已知锐角θ满足sin2θ=a,则sinθ+cosθ的值是( )
A、
| ||||
B、
| ||||
C、±
| ||||
D、
|
若f(x)是(-a,a)上的可导奇函数,且f'(x)不恒为零,则f'(x)在(-a,a)上( )
| A、必为奇函数 |
| B、必为偶函数 |
| C、是非奇非偶函数 |
| D、可能为奇函数,也可能是偶函数 |