题目内容
已知数列{an}是等差数列,且a2=-17,a5+a6=-104,又若{bn}是各项为正数的等比数列,且满足b1=2,其前n项和为Sn,b3+S3=22.
(1)求{an},{bn}的通项公式;
(2)设数列a1,b1,a2,b2,a3,b3…的前n项和为Tn,求Tn的表达式.
(1)求{an},{bn}的通项公式;
(2)设数列a1,b1,a2,b2,a3,b3…的前n项和为Tn,求Tn的表达式.
考点:数列的求和,等差数列的性质
专题:综合题,等差数列与等比数列
分析:(1)利用等差数列、等比数列的通项公式,求出基本量,即可求{an},{bn}的通项公式;
(2)利用等差数列、等比数列的求和公式,即可求Tn的表达式.
(2)利用等差数列、等比数列的求和公式,即可求Tn的表达式.
解答:
解:(1)∵数列{an}是等差数列,且a2=-17,a5+a6=-104,
∴a1+d=-17,2a1+9d=-104,
∴a1=-7,d=-10,
∴an=-7-10(n-1)=-10n+3;
∵{bn}是各项为正数的等比数列,且满足b1=2,其前n项和为Sn,b3+S3=22,
∴2q2+
=22,∴q=2,
∴bn=2n;
(2)Tn=
+
=-5n2-2n+2n+1-2.
∴a1+d=-17,2a1+9d=-104,
∴a1=-7,d=-10,
∴an=-7-10(n-1)=-10n+3;
∵{bn}是各项为正数的等比数列,且满足b1=2,其前n项和为Sn,b3+S3=22,
∴2q2+
| 2(1-q3) |
| 1-q |
∴bn=2n;
(2)Tn=
| n(-7-10n+3) |
| 2 |
| 2(1-2n) |
| 1-2 |
点评:本题考查等差数列、等比数列的通项公式、求和公式,考查学生的计算能力,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目

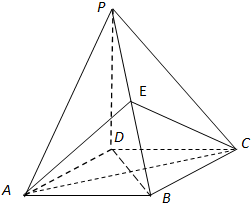 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.