题目内容
设函数f（x）=x3+ax2+bx+c和g（x）=4x2-7x+2，满足下列条件：①函数y=f（x）在x=-1处有极值；②曲线y=f（x）与y=g（x）在点（2，4）处有公共切线．
（1）求a，b，c；
（2）求函数y=f（x）的单调区间．
（1）求a，b，c；
（2）求函数y=f（x）的单调区间．
考点：利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题：综合题,导数的综合应用
分析：（1）利用极值的定义，可得b=2a-3，利用曲线y=f（x）与y=g（x）在点（2，4）处有公共切线，可得4=8+4ax+2b+c；12+4a+b=9，由3个式子求出a，b，c；
（2）利用导数的正负，求函数y=f（x）的单调区间．
（2）利用导数的正负，求函数y=f（x）的单调区间．
解答：
解：（1）函数y=f（x）在x=-1处有极值，求导f′（x）=3x2+2ax+b，把-1代入，b=2a-3；
根据曲线y=f（x）与y=g（x）在点（2，4）处有公共切线，即函数f（x）过（2，4），4=8+4ax+2b+c；
∵g′（2）=8×2-7=9
∴12+4a+b=9；
由3个式子求出a=0，b=-3，c=2；
（2）f′（x）=3x2-3
由f′（x）＞0，可得x＜-1或x＞1；由f′（x）＜0，可得-1＜x＜1，
∴函数f（x）的单调递增区间为（-∞，-1），（1，+∞）；单调递减区间为（-1，1）．
根据曲线y=f（x）与y=g（x）在点（2，4）处有公共切线，即函数f（x）过（2，4），4=8+4ax+2b+c；
∵g′（2）=8×2-7=9
∴12+4a+b=9；
由3个式子求出a=0，b=-3，c=2；
（2）f′（x）=3x2-3
由f′（x）＞0，可得x＜-1或x＞1；由f′（x）＜0，可得-1＜x＜1，
∴函数f（x）的单调递增区间为（-∞，-1），（1，+∞）；单调递减区间为（-1，1）．
点评：本题考查利用导数研究曲线上某点切线方程，考查利用导数研究函数的单调性，属于中档题．
练习册系列答案
相关题目
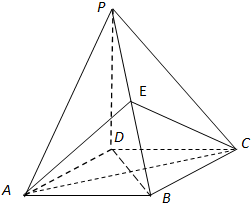如图，四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上．