题目内容
解下列方程或不等式:
(1)A2n+14=140An3
(2)AN4≥24Cn6.
(1)A2n+14=140An3
(2)AN4≥24Cn6.
考点:排列及排列数公式
专题:概率与统计
分析:(1)由已知得(2n+1)×2n(2n-1)×(2n-2)=140n(n-1)(n-2),由此能求出n=3.
(2)由已知得n(n-1)(n-2)(n-3)≥24×
,又n∈N*,且n≥6,由此能求出n.
(2)由已知得n(n-1)(n-2)(n-3)≥24×
| n(n-1)(n-2)(n-3)(n-4)(n-5) |
| 6×5×4×3×2×1 |
解答:
解:(1)∵A2n+14=140An3
∴(2n+1)×2n(2n-1)×(2n-2)=140n(n-1)(n-2),
整理,得:4n2-35n+69=0,
解得n=3,或n=
(舍)
∴n=3.
(2)∵An4≥24Cn6,
∴n(n-1)(n-2)(n-3)≥24×
,
∴
≤1,
整理,得n2-9n-10≤0,
解得-1≤n≤10,
∵n∈N*,且n≥6,
∴n的值为:6,7,8,9,10.
∴(2n+1)×2n(2n-1)×(2n-2)=140n(n-1)(n-2),
整理,得:4n2-35n+69=0,
解得n=3,或n=
| 23 |
| 4 |
∴n=3.
(2)∵An4≥24Cn6,
∴n(n-1)(n-2)(n-3)≥24×
| n(n-1)(n-2)(n-3)(n-4)(n-5) |
| 6×5×4×3×2×1 |
∴
| (n-4)(n-5) |
| 30 |
整理,得n2-9n-10≤0,
解得-1≤n≤10,
∵n∈N*,且n≥6,
∴n的值为:6,7,8,9,10.
点评:本题考查排列数公式和组合数公式的合理运用,是基础题,解题时要认真审题.

练习册系列答案
相关题目
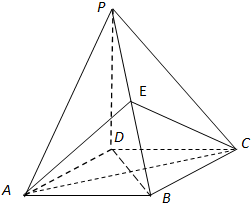 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.