题目内容
5.在平面直角坐标系xOy中,不等式组$\left\{\begin{array}{l}x≥1\\ y≥x\\ x+y-3≤0\end{array}\right.$所表示的平面区域的面积为( )| A. | $\frac{2}{9}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 由约束条件作出可行域,联立方程组求出三角形三个顶点的坐标,代入三角形面积公式得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x≥1\\ y≥x\\ x+y-3≤0\end{array}\right.$作出可行域如图: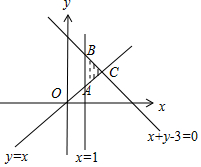
联立$\left\{\begin{array}{l}{x=1}\\{y=x}\end{array}\right.$,解得A(1,1),
联立$\left\{\begin{array}{l}{x=1}\\{x+y-3=0}\end{array}\right.$,解得B(1,2),
联立$\left\{\begin{array}{l}{y=x}\\{x+y-3=0}\end{array}\right.$,解得C($\frac{3}{2},\frac{3}{2}$).
∴平面区域的面积为$\frac{1}{2}×(2-1)×(\frac{3}{2}-1)=\frac{1}{4}$,
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.在△ABC中,角A,B,C所对的边分别为a,b,c,根据下列条件解三角形,其中有两个解的是( )
| A. | a=5,b=5,A=50° | B. | a=3,b=4,A=30° | ||
| C. | a=5,b=10,A=30° | D. | a=12,b=10,A=135° |
16.二项式${({x^2}-\frac{1}{{\sqrt{x}}})^{10}}$的展开式的二项式系数和为( )
| A. | 1 | B. | -1 | C. | 210 | D. | 0 |
20.若f(x)=2xf'(1)+x2,则f'(0)等于( )
| A. | -2 | B. | 4 | C. | 2 | D. | -4 |
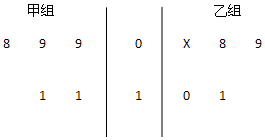 如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示
如图茎叶图记录了甲乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示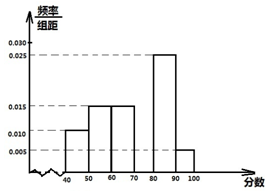 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: