题目内容
17.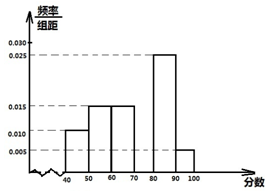 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:(1)求第四小组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)用分层抽样的方法从成绩是80分以上的学生中抽取了6人进行试卷分析,再从这6个人中选2人作学习经验介绍发言,求选出的2人中至少有1人在[90,100]的概率.
分析 (1)在频率分直方图中,小矩形的面积等于这一组的频率,根据频率的和等于1建立等式解之即可;
(2)60及以上的分数所在的第三、四、五、六组,从而求出抽样学生成绩的合格率,再利用组中值估算抽样学生的平均分即可;
(3)[80,90),[90,100]的人数是15,3.所以从成绩是80分以上(包括80分)的学生中抽取的6 人中[80,90)有5人,[90,100]中有1人,进而可求至少1人在他们在[90,100]的概率.
解答 解:(1)因为各组的频率和等于1,
故第四组的频率:
f4=1-(0.025+0.015×2+0.01+0.005)×10=0.03,
直方图如右所示.
(2)依题意,60及以上的分数所在的第三、四、五、六组,频率和为:
(0.015+0.03+0.025+0.005)×10=0.75
所以,抽样学生成绩的合格率是75%,
利用组中值估算抽样学生的平均分为:
45•f1+55•f2+65•f3+75•f4+85•f5+95•f6
=45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,
估计这次考试的平均分是71分.
(3)[80,90),[90,100]的人数是15,3.
所以从成绩是80分以上(包括80分)的学生中抽取的6人中[80,90)有5人,[90,100]中有1人,
从这6人中选2人共有15种选法,至少有1人在[90,100]的选法有5种,
所以,至少1人在他们在[90,100]的概率为$\frac{5}{15}$=$\frac{1}{3}$.
点评 本题主要考查了频率及频率分布直方图,考查运用统计知识解决简单实际问题的能力,数据处理能力和运用意识.

练习册系列答案
相关题目
5.在平面直角坐标系xOy中,不等式组$\left\{\begin{array}{l}x≥1\\ y≥x\\ x+y-3≤0\end{array}\right.$所表示的平面区域的面积为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
12. 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为M1,众数为M2,平均值为$\overline x$,则( )
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为M1,众数为M2,平均值为$\overline x$,则( )
 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为M1,众数为M2,平均值为$\overline x$,则( )
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为M1,众数为M2,平均值为$\overline x$,则( )| A. | M1=M2=$\overline x$ | B. | M1=M2<$\overline x$ | C. | M1<M2<$\overline x$ | D. | M2<M1<$\overline x$ |
9.在△ABC中,B=30°,AB=$\sqrt{3}$,AC=1,则△ABC的面积是( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$或$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$ |
6.已知函数$f(x)=\left\{\begin{array}{l}{log_2}({{x^2}+x+a}),x≥1\\ 1-{x^2},x<1\end{array}\right.$的值域为R,则常数a的取值范围是( )
| A. | [0,+∞) | B. | (-2,-1] | C. | (-2,0] | D. | (-∞,0] |
7.给出如图所示的程序,执行该程序时,若输入的x为3,则输出的y值是( )


| A. | 3 | B. | 6 | C. | 9 | D. | 27 |