题目内容
10.若关于x的不等式(2a-b)x+(a+b)>0的解集为{x|x>-3},则$\frac{b}{a}$=$\frac{5}{4}$.分析 根据题意,得出关于a、b的关系式,即可求出$\frac{b}{a}$的值.
解答 解:关于x的不等式(2a-b)x+(a+b)>0的解集为{x|x>-3},
∴(2a-b)x>-(a+b),
∴$\left\{\begin{array}{l}{2a-b>0}\\{\frac{-a-b}{2a-b}=-3}\end{array}\right.$,
∴a+b=3(2a-b),
∴$\frac{b}{a}$=$\frac{5}{4}$.
故答案为:$\frac{5}{4}$.
点评 本题考查了不等式的解法与应用问题,是基础题.

练习册系列答案
相关题目
20.若集合A={x|x2≤4},B={x|x≥0}.则A∩B=( )
| A. | {x|0≤x≤2} | B. | {x|x≥-2} | C. | {0,1,2} | D. | {1,2} |
1.下列命题中正确的是( )
| A. | 终边在x轴负半轴上的角是零角 | |
| B. | 三角形的内角必是第一、二象限内的角 | |
| C. | 不相等的角的终边一定不相同 | |
| D. | 若β=α+k•360°(k∈Z),则α与β终边相同 |
5.在平面直角坐标系xOy中,不等式组$\left\{\begin{array}{l}x≥1\\ y≥x\\ x+y-3≤0\end{array}\right.$所表示的平面区域的面积为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
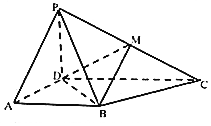 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是正三角形,底面ABCD是直角梯形,AB∥CD,CD⊥AD,CD=2AB=2AD=2,M为PC的中点.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是正三角形,底面ABCD是直角梯形,AB∥CD,CD⊥AD,CD=2AB=2AD=2,M为PC的中点. 如图,矩形ABCD中,$AB=2\sqrt{2}$,$AD=\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,$AB=2\sqrt{2}$,$AD=\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.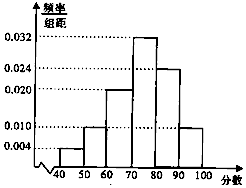 某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.