题目内容
在△ABC中,a,b,c分别为角A,B,C的对边,若△ABC的面积为
,∠A=15°,则
+
的值为( )
| a2 |
| 4 |
| b |
| c |
| c |
| b |
A、
| ||
B、2
| ||
C、2
| ||
D、
|
考点:解三角形
专题:解三角形
分析:由面积公式可得2bc=
,结合余弦定理可得
+
=
=2(sinA+cosA)=2
sin(A+45°),代值计算可得.
| a2 |
| sinA |
| b |
| c |
| c |
| b |
| b2+c2 |
| bc |
| 2 |
解答:
解:由题意可得△ABC的面积S=
bcsinA=
,∴2bc=
,
∴由余弦定理可得cosA=
=
-
=
-
=
-sinA,
∴
+
=
=2(sinA+cosA)
=2
sin(A+45°)=2
sin60°=
故选:D
| 1 |
| 2 |
| a2 |
| 4 |
| a2 |
| sinA |
∴由余弦定理可得cosA=
| b2+c2-a2 |
| 2bc |
| b2+c2 |
| 2bc |
| a2 |
| 2bc |
=
| b2+c2 |
| 2bc |
| a2 | ||
|
| b2+c2 |
| 2bc |
∴
| b |
| c |
| c |
| b |
| b2+c2 |
| bc |
=2
| 2 |
| 2 |
| 6 |
故选:D
点评:本题考查解三角形,涉及余弦定理和三角形的面积公式,属中档题.

练习册系列答案
相关题目
设双曲线
-
=1(a>0,b>0)的离心率为
,且它的一个焦点与抛物线y2=24x的焦点重合,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知
,
满足:|
|=3,|
|=2,|
+
|=4,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
| C、3 | ||
D、
|
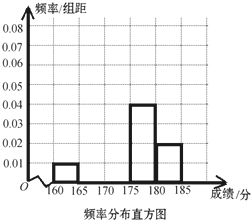 永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示:
永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示: