题目内容
若圆锥的底面半径为2,轴截面为等腰直角三角形,则圆锥的全面积为 .
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:根据圆锥的底面半径及轴截面为等腰直角三角形,然后求出圆锥的母线,即可求解圆锥的全面积.
解答:
解:∵圆锥的轴截面是等腰直角三角形,圆锥的底面半径为2,
圆锥的轴截面是等腰直角三角形,
∴圆锥的母线长为2
,
∴圆锥的侧面积S=πr(r+l)=(4+4
)π,
故答案为:(4+4
)π
圆锥的轴截面是等腰直角三角形,
∴圆锥的母线长为2
| 2 |
∴圆锥的侧面积S=πr(r+l)=(4+4
| 2 |
故答案为:(4+4
| 2 |
点评:本题考查圆锥的计算,得到圆锥的底面半径是解决本题的突破点;注意圆锥的全面积S=πr(r+l)的理解和应用.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
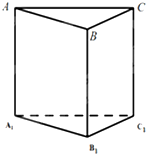 如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2
如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2| 34 |
A、
| ||||
B、
| ||||
C、360
| ||||
D、
|
在三棱锥P-ABC中,PA=PB=PC,底面△ABC是正三角形,M、N分别是侧棱PB、PC的中点.若平面AMN⊥平面PBC,则侧棱PB与平面ABC所成角的正切值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,a,b,c分别为角A,B,C的对边,若△ABC的面积为
,∠A=15°,则
+
的值为( )
| a2 |
| 4 |
| b |
| c |
| c |
| b |
A、
| ||
B、2
| ||
C、2
| ||
D、
|
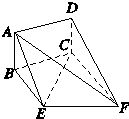 如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=