题目内容
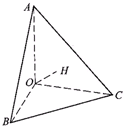 如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有
如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有①底面△ABC是锐角三角形;
②四面体AOCB的对棱互相垂直;
③四面体AOCB的外接球半径R=
| 1 |
| 2 |
| a2+b2+c2 |
④点H是△ABC的垂心;
⑤
| 2 |
| OH2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
考点:空间中直线与直线之间的位置关系,棱锥的结构特征
专题:空间位置关系与距离
分析:①由向量的数量积能求出底面△ABC是锐角三角形;②由题意利用线面垂直能求出OB⊥AC,OA⊥BC,OC⊥AB;③以点O为长方体的一个顶点,OA、OB、OC为长方体的三棱作长方体,则四面体OABC的外接球就是长方体的外接球;④由已知条件能推导出BC⊥AH,CH⊥AB,所以H是△ABC的垂心;⑤由已知条件推导出
=
+
+
.
| 1 |
| OH2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
解答:
 解:①
解:①
•
=(
-
)•(
-
)=
2=|
|2>0,
知A为锐角,同理B,C也是锐角,故①正确;
②由题意知OB⊥平面OAC,从而OB⊥AC,
同理可得:OA⊥BC,OC⊥AB,故②正确;
③以点O为长方体的一个顶点,OA、OB、OC为长方体的三棱作长方体,
则四面体OABC的外接球就是长方体的外接球,
且R=
,故③正确.
④连结AH,并延长交BC于D,连结OD,OH⊥平面ABC,
OA⊥BC,所以BC⊥AH,同理,CH⊥AB,
所以H是△ABC的垂心,故④正确.
⑤在直角△AOD中,AO•OD=OH•AD,AO2•OD2=OH2•(AO2+OD2),
=
+
,同理,在△BOC中,
=
+
,
所以
=
+
+
,故⑤错误.
故答案为:①②③④.
 解:①
解:①| AB |
| AC |
| OB |
| OA |
| OC |
| OA |
| OA |
| OA |
知A为锐角,同理B,C也是锐角,故①正确;
②由题意知OB⊥平面OAC,从而OB⊥AC,
同理可得:OA⊥BC,OC⊥AB,故②正确;
③以点O为长方体的一个顶点,OA、OB、OC为长方体的三棱作长方体,
则四面体OABC的外接球就是长方体的外接球,
且R=
| 1 |
| 2 |
| a2+b2+c2 |
④连结AH,并延长交BC于D,连结OD,OH⊥平面ABC,
OA⊥BC,所以BC⊥AH,同理,CH⊥AB,
所以H是△ABC的垂心,故④正确.
⑤在直角△AOD中,AO•OD=OH•AD,AO2•OD2=OH2•(AO2+OD2),
| 1 |
| OH2 |
| 1 |
| OA2 |
| 1 |
| OD2 |
| 1 |
| OD2 |
| 1 |
| OB2 |
| 1 |
| OC2 |
所以
| 1 |
| OH2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
故答案为:①②③④.
点评:本题考查命题的真假判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
半径为R的球的内接正三棱柱的三个侧面积之和的最大值为( )
A、3
| ||
B、
| ||
C、2
| ||
D、
|
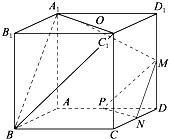 如图,在正方体ABCD-A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,M、N、P分别为所在边的中点,O为面对角线A1C1的中点.