题目内容
已知向量
,
的夹角为
,且|
|=4,(
+
)•(2
-3
)=12,则向量
在向量
方向上的投影是( )
| a |
| b |
| π |
| 4 |
| a |
| 1 |
| 2 |
| a |
| b |
| a |
| b |
| b |
| a |
A、
| ||
| B、4 | ||
C、4
| ||
| D、1 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积的定义和性质、投影的定义即可得出.
解答:
解:∵向量
,
的夹角为
,且|
|=4,
∴
•
=|
| |
|cos
=2
|
|.
∵(
+
)•(2
-3
)=12,
∴
2+
•
-3
2=12,
化为3|
|2-
|
|-4=0,
解得|
|=
.
则向量
在向量
方向上的投影=|
|cos
=
×
=1.
故选:D.
| a |
| b |
| π |
| 4 |
| a |
∴
| a |
| b |
| a |
| b |
| π |
| 4 |
| 2 |
| b |
∵(
| 1 |
| 2 |
| a |
| b |
| a |
| b |
∴
| a |
| 1 |
| 2 |
| a |
| b |
| b |
化为3|
| b |
| 2 |
| b |
解得|
| b |
| 2 |
则向量
| b |
| a |
| b |
| π |
| 4 |
| 2 |
| ||
| 2 |
故选:D.
点评:本题考查了数量积的定义和性质、投影的定义,属于中档题.

练习册系列答案
相关题目
已知⊙C:x2+y2=9中弦AB的长为3
,则
•
=( )
| 2 |
| AB |
| AC |
| A、0 | ||
| B、3 | ||
| C、9 | ||
D、9
|
已知P是△ABC所在的平面内一点,AB=4,
+
+
=
,
•
=
•
=
•
,若点D、E分别满足
=-
,
=3
,则
•
=( )
| PA |
| PB |
| PC |
| 0 |
| PA |
| PB |
| PB |
| PC |
| PC |
| PA |
| DC |
| AC |
| BE |
| EC |
| AP |
| DE |
| A、8 | ||
B、
| ||
C、-4
| ||
| D、-8 |
已知m为一条直线,α、β为两个不同的平面,则下列说法正确的是( )
| A、若m∥α,α⊥β,则m⊥β |
| B、若m⊥α,α∥β,则m⊥β |
| C、若m∥α,α∥β,则m∥β |
| D、若m∥α,m∥β,则α∥β |
某人忘记了自己的文档密码,但记得该密码是由一个2,一个9,两个6组成的四位数,于是用这四个数随意排成一个四位数,输入电脑尝试,那么他找到自己的文档密码最多尝试次数为( )
| A、36 | B、24 | C、18 | D、12 |
若复数z满足
=2+i(其中i为虚数单位),则z的共轭复数为( )
| z+i |
| i |
| A、-1-i | B、1-i |
| C、-1+i | D、1+i |
在长为10厘米的线段AB上任取一点G,以AG为半径作圆,则圆的面积介于36π平方厘米到64π平方厘米的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
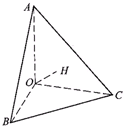 如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有
如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有