题目内容
已知函数f(x)=
则方程f(x)=ax恰有两个不同实数根时,实数a的取值范围是 .
|
考点:利用导数研究曲线上某点切线方程,函数的零点与方程根的关系,分段函数的应用
专题:综合题,导数的综合应用
分析:由题意,方程f(x)=ax恰有两个不同实数根,等价于y=f(x)与y=ax有2个交点,又a表示直线y=ax的斜率,求出a的取值范围.
解答:
解:∵方程f(x)=ax恰有两个不同实数根,
∴y=f(x)与y=ax有2个交点,
又∵a表示直线y=ax的斜率,
∴y′=
,
设切点为(x0,y0),k=
,
∴切线方程为y-y0=
(x-x0),
而切线过原点,∴y0=1,x0=e,k=
,
∴直线l1的斜率为
,
又∵直线l2与y=
x+1平行,
∴直线l2的斜率为
,
∴实数a的取值范围是[
,
)
故答案为:[
,
).
∴y=f(x)与y=ax有2个交点,
又∵a表示直线y=ax的斜率,
∴y′=
| 1 |
| x |
设切点为(x0,y0),k=
| 1 |
| x0 |
∴切线方程为y-y0=
| 1 |
| x0 |
而切线过原点,∴y0=1,x0=e,k=
| 1 |
| e |
∴直线l1的斜率为
| 1 |
| e |
又∵直线l2与y=
| 1 |
| 4 |
∴直线l2的斜率为
| 1 |
| 4 |
∴实数a的取值范围是[
| 1 |
| 4 |
| 1 |
| e |
故答案为:[
| 1 |
| 4 |
| 1 |
| e |
点评:本题考查了函数的图象与性质的应用问题,考查函数与方程的关系,是易错题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
已知函数f(x)的导函数为f′(x),对?x∈R,f′(x)-f(x)<0,则对任意正数a有( )
A、
| ||
B、
| ||
| C、eaf(a)>f(0) | ||
| D、eaf(a)<f(0) |
已知⊙C:x2+y2=9中弦AB的长为3
,则
•
=( )
| 2 |
| AB |
| AC |
| A、0 | ||
| B、3 | ||
| C、9 | ||
D、9
|
若复数z满足
=2+i(其中i为虚数单位),则z的共轭复数为( )
| z+i |
| i |
| A、-1-i | B、1-i |
| C、-1+i | D、1+i |
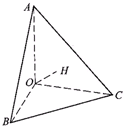 如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有
如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有