题目内容
若a>1,设函数f(x)=ax+x-4的零点为m,g(x)=logax+x-4的零点为n,则
+
的最小值为 .
| 1 |
| m |
| 1 |
| n |
考点:函数零点的判定定理,基本不等式
专题:函数的性质及应用
分析:构建函数F(x)=ax,G(x)=logax,h(x)=4-x,则h(x)与F(x),G(x)的交点A,B的横坐标分别为m、n,注意到F(x)=ax,G(x)=logax,关于直线y=x对称,可得m+n=4,再用“1”的代换,利用基本不等式,即可得出结论.
解答:
解:由题意,构建函数F(x)=ax,G(x)=logax,h(x)=4-x,
则h(x)与F(x),G(x)的交点A,B的横坐标分别为m、n.
注意到F(x)=ax,G(x)=logax,关于直线y=x对称,可以知道A,B关于y=x对称,
由于y=x与y=4-x交点的横坐标为2,∴m+n=4.
则
+
=
(
+
)(m+n)=
(2+
+
)≥
(2+2)=1,
当且仅当m=n=2时,等号成立,故
+
的最小值为1,
故答案为:1.
则h(x)与F(x),G(x)的交点A,B的横坐标分别为m、n.
注意到F(x)=ax,G(x)=logax,关于直线y=x对称,可以知道A,B关于y=x对称,
由于y=x与y=4-x交点的横坐标为2,∴m+n=4.
则
| 1 |
| m |
| 1 |
| n |
| 1 |
| 4 |
| 1 |
| m |
| 1 |
| n |
| 1 |
| 4 |
| n |
| m |
| m |
| n |
| 1 |
| 4 |
当且仅当m=n=2时,等号成立,故
| 1 |
| m |
| 1 |
| n |
故答案为:1.
点评:本题考查函数的零点,考查基本不等式的运用,考查学生分析转化问题的能力,求出m+n=4,正确运用基本不等式是关键,属于基础题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
已知⊙C:x2+y2=9中弦AB的长为3
,则
•
=( )
| 2 |
| AB |
| AC |
| A、0 | ||
| B、3 | ||
| C、9 | ||
D、9
|
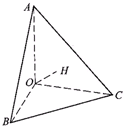 如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有
如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有