题目内容
半径为R的球的内接正三棱柱的三个侧面积之和的最大值为( )
A、3
| ||
B、
| ||
C、2
| ||
D、
|
考点:球内接多面体
专题:综合题,空间位置关系与距离
分析:设正三棱柱的底面边长为a,侧棱长为l,表示内接正三棱柱的三个侧面积之和,进而结合基本不等式可得S的最值.
解答:
解:设正三棱柱的底面边长为a,侧棱长为l,则得底面半径r=
a,(
)2+r2=R2,
∴l2=4R2-
a2,即l=2
.
∴S侧=3al=6a
=6
≤6
=3
R2.
即半径为R的球的内接正三棱柱的三个侧面积之和的最大值是3
R2.
故选:A.
| ||
| 3 |
| l |
| 2 |
∴l2=4R2-
| 4 |
| 3 |
R2-
|
∴S侧=3al=6a
R2-
|
3•
|
≤6
3•(
|
| 3 |
即半径为R的球的内接正三棱柱的三个侧面积之和的最大值是3
| 3 |
故选:A.
点评:本题考查的知识点是球的内接多面体,基本不等式,正确表示内接正三棱柱的三个侧面积之和是解答的关键.

练习册系列答案
相关题目
已知函数f(x)的导函数为f′(x),对?x∈R,f′(x)-f(x)<0,则对任意正数a有( )
A、
| ||
B、
| ||
| C、eaf(a)>f(0) | ||
| D、eaf(a)<f(0) |
已知向量
=(3,4),
=(-2,1),若(
+x
)⊥
,则实数x为( )
| a |
| b |
| a |
| b |
| b |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知⊙C:x2+y2=9中弦AB的长为3
,则
•
=( )
| 2 |
| AB |
| AC |
| A、0 | ||
| B、3 | ||
| C、9 | ||
D、9
|
已知P是△ABC所在的平面内一点,AB=4,
+
+
=
,
•
=
•
=
•
,若点D、E分别满足
=-
,
=3
,则
•
=( )
| PA |
| PB |
| PC |
| 0 |
| PA |
| PB |
| PB |
| PC |
| PC |
| PA |
| DC |
| AC |
| BE |
| EC |
| AP |
| DE |
| A、8 | ||
B、
| ||
C、-4
| ||
| D、-8 |
在长为10厘米的线段AB上任取一点G,以AG为半径作圆,则圆的面积介于36π平方厘米到64π平方厘米的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
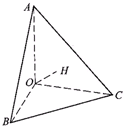 如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有
如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有