题目内容
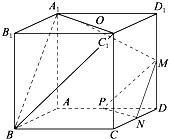如图，在正方体ABCD-A1B1C1D1中，M、N、P分别为所在边的中点，O为面对角线A1C1的中点．（1）求证：面MNP∥面A1C1B．
（2）求证：OM⊥面A1BC1．
考点：直线与平面垂直的判定,平面与平面平行的判定
专题：空间位置关系与距离
分析：（1）连结D1C，由三角形中位线定理得MN∥D1C，MP∥C1B，由此能证明面MNP∥面A1C1B．
（2）连结C1M和A1M，设正方体的边长为a，连结BO和BM，由勾股定理得BO⊥MO．由此能证明MO⊥面A1C1B．
（2）连结C1M和A1M，设正方体的边长为a，连结BO和BM，由勾股定理得BO⊥MO．由此能证明MO⊥面A1C1B．
解答：
证明：（1）连结D1C，MN为△DD1C的中位线，∴MN∥D1C．…（2分）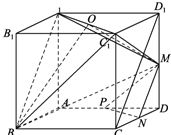
又∵D1C∥A1B∴MN∥A1B．同理MP∥C1B．…（4分）
而MN与MP相交，MN，MP?面MNP，A1B，A1B?面A1C1B．
∴面MNP∥面A1C1B．…（6分）
（2）连结C1M和A1M，设正方体的边长为a，
∵正方体ABCD-A1B1C1D1，∴C1M=A1M，
又∵O为A1C1的中点，
∴A1C1⊥MO…（8分）
连结BO和BM，在三角形BMO中，
OB=
a，MO=
a，BM=
a，
∴OB2+MO2=MB2，
即BO⊥MO．而A1C1，BO?面A1C1B，
∴MO⊥面A1C1B．…（12分）
又∵D1C∥A1B∴MN∥A1B．同理MP∥C1B．…（4分）
而MN与MP相交，MN，MP?面MNP，A1B，A1B?面A1C1B．
∴面MNP∥面A1C1B．…（6分）
（2）连结C1M和A1M，设正方体的边长为a，
∵正方体ABCD-A1B1C1D1，∴C1M=A1M，
又∵O为A1C1的中点，
∴A1C1⊥MO…（8分）
连结BO和BM，在三角形BMO中，
OB=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
∴OB2+MO2=MB2，
即BO⊥MO．而A1C1，BO?面A1C1B，
∴MO⊥面A1C1B．…（12分）
点评：本题考查面面平行的证明，考查直线与平面垂直的证明，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
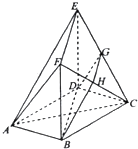如图，在多面体ABCDEF中，底面ABCD是边长为2的正方形，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，G和H分别是CE，CF的中点．
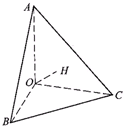如图，在四面体AOCB中，∠AOB=∠AOC=∠BOC=90°，OA=a，OB=b，OC=c，直角顶点O在底面ABC上的射影是H，则下列命题正确的有