题目内容
如果随机变量ξ的概率分布律由下表给出:则Dξ= .
| x | 0 |
| π | ||||||
| P(ξ=x) |
|
|
|
考点:离散型随机变量的期望与方差
专题:计算题,概率与统计
分析:由题意及随机变量ξ的概率分布表,可以先利用期望定义求出期望Eξ的值,再由方差的定义求出其方差即可.
解答:
解:由题意及表格可得:Eξ=0×
+
×
+π×
=
,
Dξ=
×(0-
)2+
×(
-
)2+
×(π-
)2=
.
故答案为:
.
| 1 |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| π |
| 2 |
Dξ=
| 1 |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 1 |
| 4 |
| π |
| 2 |
| π2 |
| 8 |
故答案为:
| π2 |
| 8 |
点评:此题考查了离散型随机变量的期望与方差的定义及计算,重点考查了学生的计算能力及公式的正确使用.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知函数f(x)的导函数为f′(x),对?x∈R,f′(x)-f(x)<0,则对任意正数a有( )
A、
| ||
B、
| ||
| C、eaf(a)>f(0) | ||
| D、eaf(a)<f(0) |
已知m为一条直线,α、β为两个不同的平面,则下列说法正确的是( )
| A、若m∥α,α⊥β,则m⊥β |
| B、若m⊥α,α∥β,则m⊥β |
| C、若m∥α,α∥β,则m∥β |
| D、若m∥α,m∥β,则α∥β |
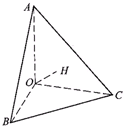 如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有
如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有