题目内容
A是曲线C1:
+
=1与C2:
-y2=1的一个交点,且A到C1的两焦点的距离之和为m,到C2两焦点距离之差的绝对值为n,则lg(m+n)= .
| x2 |
| 9 |
| y2 |
| 4 |
| x2 |
| 4 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:利用椭圆的定义,求出m,利用双曲线的定义,求出n,即可得出结论.
解答:
解:由题意,m是点A到C1:
+
=1两焦点的距离之和,
∴m=6,
∵n是点A到C2:
-y2=1两焦点距离之差的绝对值,
∴n=4,
∴m+n=10,
∴lg(m+n)=1.
故答案为:1.
| x2 |
| 9 |
| y2 |
| 4 |
∴m=6,
∵n是点A到C2:
| x2 |
| 4 |
∴n=4,
∴m+n=10,
∴lg(m+n)=1.
故答案为:1.
点评:本题考查椭圆、双曲线的定义,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
已知向量
=(3,4),
=(-2,1),若(
+x
)⊥
,则实数x为( )
| a |
| b |
| a |
| b |
| b |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
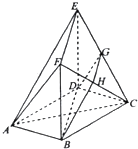 如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE,CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE,CF的中点.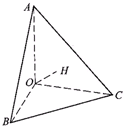 如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有
如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有