题目内容
函数f(ax+b)=2m-f(-ax+c)的对称中心为 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数的对称中心求法,求得对称中心.
解答:
解:∵f(ax+b)=2m-f(-ax+c),
∴
[f(ax+b)+f(-ax+c)]=m,
又
[(ax+b)+(-ax+c)]=
∴点(ax+b,f(ax+b)),与点(-ax+c,f(-ax+c))关于点(
,m)对称.
∴函数f(x)的图象的对称中心为(
,m),
故答案为;(
,m)
∴
| 1 |
| 2 |
又
| 1 |
| 2 |
| b+c |
| 2 |
∴点(ax+b,f(ax+b)),与点(-ax+c,f(-ax+c))关于点(
| b+c |
| 2 |
∴函数f(x)的图象的对称中心为(
| b+c |
| 2 |
故答案为;(
| b+c |
| 2 |
点评:考查学生灵活运用函数图象对称性问题,掌握如何求对称中心是关键,属于基础题,本题也求对称的中心的一个公式.

练习册系列答案
相关题目
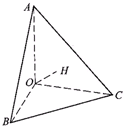 如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有
如图,在四面体AOCB中,∠AOB=∠AOC=∠BOC=90°,OA=a,OB=b,OC=c,直角顶点O在底面ABC上的射影是H,则下列命题正确的有