题目内容
已知α为锐角，且cos（α+
）=
，则cosα的值为（ ）
| π |
| 6 |
| 4 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：两角和与差的余弦函数
专题：计算题,三角函数的求值
分析：利用α为锐角，且cos（α+
）=
，可得sin（α+
）=
，由cosα=cos[（α+
）-
]，利用差角的余弦公式，即可求cosα的值．
| π |
| 6 |
| 4 |
| 5 |
| π |
| 6 |
| 3 |
| 5 |
| π |
| 6 |
| π |
| 6 |
解答：
解：∵α为锐角，且cos（α+
）=
，
∴sin（α+
）=
，
∴cosα=cos[（α+
）-
]
=cos（α+
）cos
+sin（α+
）sin
=
•
+
•
=
．
故选：A．
| π |
| 6 |
| 4 |
| 5 |
∴sin（α+
| π |
| 6 |
| 3 |
| 5 |
∴cosα=cos[（α+
| π |
| 6 |
| π |
| 6 |
=cos（α+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
=
4
| ||
| 10 |
故选：A．
点评：本题考查两角和与差的余弦函数，考查角的变换，考查学生的计算能力，利用cosα=cos[（α+
）-
]是关键．
| π |
| 6 |
| π |
| 6 |
练习册系列答案
阅读快车系列答案
相关题目
已知在△ABC中满足：tanA•tanB=1+
（tanA+tanB），则角C等于（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若直线（2n+1）x+（n+5）y-6=0和（n-3）x+（1-2n）y-7=0垂直，则n的值为（ ）
A、
| ||
B、-
| ||
| C、1 | ||
D、
|
已知A（2，2）、B（-1，3），若直线l过点P（1，1）且与线段AB相交，则直线l的倾斜角α的取值范围是（ ）
A、α≥
| ||||||||
B、
| ||||||||
| C、-1≤α≤1 | ||||||||
D、
|
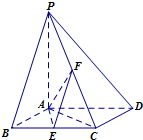如图，已知四棱锥P-ABCD中，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点．
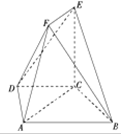如图所示的几何体，四边形ABCD中，有AB∥CD，∠BAC=30°，AB=2CD=2，CB=1．点E在平面ABCD内的射影是点C，EF∥AC，且AC=2EF．