题目内容
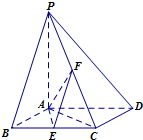 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.(1)证明:AE⊥平面PAD;
(2)取AB=2,若H为PD上的动点,EH与平面PAD所成最大角的正切值为
| ||
| 2 |
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间角
分析:(1)由已知条件推导出△ABC为正三角形,从而得到AE⊥BC,AE⊥AD,再由PA⊥平面ABCD,得到PA⊥AE,由此能证明AE⊥平面PAD.
(2)法一:H为PD上任意一点,连接AH,EH,则∠EHA为EH与平面PAD所成的角,当AH最短时,即当AH⊥PD时,∠EHA最大,由此能求出二面角E-AF-C的余弦值.
(2)法二:由(1)知AE,AD,AP两两垂直,以A为坐标原点,建立空间直角坐标系.利用向量法能求出二面角E-AF-C的余弦值.
(2)法一:H为PD上任意一点,连接AH,EH,则∠EHA为EH与平面PAD所成的角,当AH最短时,即当AH⊥PD时,∠EHA最大,由此能求出二面角E-AF-C的余弦值.
(2)法二:由(1)知AE,AD,AP两两垂直,以A为坐标原点,建立空间直角坐标系.利用向量法能求出二面角E-AF-C的余弦值.
解答:
(本小题满分13分)
(1)证明:∵四边形ABCD为菱形,∠ABC=60°,
∴△ABC为正三角形,∵E为BC的中点,
∴AE⊥BC…(1分)
又∵BC∥AD,∴AE⊥AD…(2分)
∵PA⊥平面ABCD,AE?平面ABCD,
∴PA⊥AE…(3分)
而PA?平面PAD,AD?平面PAD,PA∩AD=A,
∴AE⊥平面PAD.…(5分)
(2)解法一:H为PD上任意一点,连接AH,EH,
由(1)知AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角,…(6分)
在RT△EAH中,AE=
,
∴当AH最短时,即当AH⊥PD时,∠EHA最大.…(7分)
此时tan∠EHA=
=
=
,∴AH=
,
又∵AD=2,∴∠ADH=45°,∴PA=2…(8分)
∵PA⊥平面ABCD,PA?平面PAC,
∴平面PAC⊥平面ABCD,
过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连接ES,则∠ESO为二面角E-AF-C的平面角,…(10分)
在RT△AOE中,EO=AE•sin300=
,AO=AE•cos300=
,
又F是PC的中点,在RT△ASO中,SO=AO•sin450=
,
又SE=
=
,…(11分)
在RT△ESO中,cos∠ESO=
=
即所求二面角的余弦值为
.…(13分)
(2)解法二:由(1)可知AE,AD,AP两两垂直,
以A为坐标原点,建立如图所示的空间直角坐标系.
设AP=a,则A(0,0,0),B(
,1,0),C(
,1,0),D(0,2,0),
P(0,0,a),E(
,0,0),F(
,
,
),H(0,2-2λ,aλ)(其中λ∈[0,1]),…(6分)
∴
=(
,2(λ-1),-aλ),
面PAD的法向量为
=(1,0,0),
sin2θ=|cos<
,
>|2=
=
,
∵EH与平面PAD所成最大角的正切值为
…(7分)
∴sin2θ=
的最大值为
,
即f(a)=(a2+4)λ2-8λ+7在λ∈[0,1]的最小值为5,
∵函数f(a)对称轴λ=
∈(0,1),
∴f(a)min=f(
)=5,解得a=2…(9分)
∴
=(
,0,0),
=(
,
,1)
设平面AEF的一个法向量为
=(x1,y1,z1 ),则
∴
,取z1=-1,则
=(0,2,-1)…(11分)
=(-
,3,0)为平面AFC的一个法向量.…(12分)
∴cos<
,
>=
=
∴所求二面角的余弦值为
…(13分)
(1)证明:∵四边形ABCD为菱形,∠ABC=60°,
∴△ABC为正三角形,∵E为BC的中点,
∴AE⊥BC…(1分)
又∵BC∥AD,∴AE⊥AD…(2分)
∵PA⊥平面ABCD,AE?平面ABCD,
∴PA⊥AE…(3分)
而PA?平面PAD,AD?平面PAD,PA∩AD=A,
∴AE⊥平面PAD.…(5分)
(2)解法一:H为PD上任意一点,连接AH,EH,
由(1)知AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角,…(6分)
在RT△EAH中,AE=
| 3 |
∴当AH最短时,即当AH⊥PD时,∠EHA最大.…(7分)
此时tan∠EHA=
| AE |
| AH |
| ||
| AH |
| ||
| 2 |
| 2 |
又∵AD=2,∴∠ADH=45°,∴PA=2…(8分)
∵PA⊥平面ABCD,PA?平面PAC,
∴平面PAC⊥平面ABCD,
过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连接ES,则∠ESO为二面角E-AF-C的平面角,…(10分)
在RT△AOE中,EO=AE•sin300=
| ||
| 2 |
| 3 |
| 2 |
又F是PC的中点,在RT△ASO中,SO=AO•sin450=
3
| ||
| 4 |
又SE=
| EO2+SO2 |
| ||
| 4 |

在RT△ESO中,cos∠ESO=
| SO |
| SE |
| ||
| 5 |
即所求二面角的余弦值为
| ||
| 5 |
(2)解法二:由(1)可知AE,AD,AP两两垂直,
以A为坐标原点,建立如图所示的空间直角坐标系.
设AP=a,则A(0,0,0),B(
| 3 |
| 3 |
P(0,0,a),E(
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| a |
| 2 |
∴
| HE |
| 3 |
面PAD的法向量为
| n |
sin2θ=|cos<
| n |
| HE |
| 3 |
| 3+4(λ-1)2+a2λ2 |
| 3 |
| (a2+4)λ2-8λ+7 |
∵EH与平面PAD所成最大角的正切值为
| ||
| 2 |
∴sin2θ=
| 3 |
| (a2+4)λ2-8λ+7 |
| 3 |
| 5 |
即f(a)=(a2+4)λ2-8λ+7在λ∈[0,1]的最小值为5,
∵函数f(a)对称轴λ=
| 4 |
| a2+4 |
∴f(a)min=f(
| 4 |
| a2+4 |
∴
| AE |
| 3 |
| AF |
| ||
| 2 |
| 1 |
| 2 |
设平面AEF的一个法向量为
| m |
|
∴
|
| m |
| BD |
| 3 |
∴cos<
| m |
| BD |
| ||||
|
|
| ||
| 5 |
∴所求二面角的余弦值为
| ||
| 5 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的合理运用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
将函数y=
sinx+
cosx(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| 1 |
| 4 |
| ||
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知p:xy=0,q:x=0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知α为锐角,且cos(α+
)=
,则cosα的值为( )
| π |
| 6 |
| 4 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
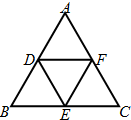 如图,已知D,E,F是正△ABC三边的中点,由A,B,C,D,E,F六点中的两点构成的向量中与
如图,已知D,E,F是正△ABC三边的中点,由A,B,C,D,E,F六点中的两点构成的向量中与