题目内容
如果对定义在R上的函数f(x),对任意x1≠x2,都有x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1)则称函数f(x)为“H函数”.给出下列函数:
①y=-x3+x+1;
②y=3x-2(sinx-cosx);
③y=ex+1;
④f(x)=
.
其中函数式“H函数”的个数是( )
①y=-x3+x+1;
②y=3x-2(sinx-cosx);
③y=ex+1;
④f(x)=
|
其中函数式“H函数”的个数是( )
| A、4 | B、3 | C、2 | D、1 |
考点:函数单调性的性质,函数的图象
专题:计算题,函数的性质及应用
分析:不等式x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1)等价为(x1-x2)[f(x1)-f(x2)]>0,即满足条件的函数为单调递增函数,判断函数的单调性即可得到结论.
解答:
解:∵对于任意给定的不等实数x1,x2,不等式x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1)恒成立,
∴不等式等价为(x1-x2)[f(x1)-f(x2)]>0恒成立,
即函数f(x)是定义在R上的增函数.
①y=-x3+x+1;y'=-3x2+1,则函数在定义域上不单调.
②y=3x-2(sinx-cosx);y'=3-2(cosx+sinx)=3-2
sin(x+
)>0,函数单调递增,满足条件.
③y=ex+1为增函数,满足条件.
④f(x)=
,当x>0时,函数单调递增,当x<0时,函数单调递减,不满足条件.
综上满足“H函数”的函数为②③,
故选C.
∴不等式等价为(x1-x2)[f(x1)-f(x2)]>0恒成立,
即函数f(x)是定义在R上的增函数.
①y=-x3+x+1;y'=-3x2+1,则函数在定义域上不单调.
②y=3x-2(sinx-cosx);y'=3-2(cosx+sinx)=3-2
| 2 |
| π |
| 4 |
③y=ex+1为增函数,满足条件.
④f(x)=
|
综上满足“H函数”的函数为②③,
故选C.
点评:本题主要考查函数单调性的应用,将条件转化为函数的单调性的形式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义两种运算a⊕b=ab,a?b=a2+b2,则f(x)=
为( )
| 2⊕x |
| x?2-2 |
| A、奇函数 |
| B、偶函数 |
| C、既不是奇函数又不是偶函数 |
| D、既是奇函数又是偶函数 |
将4名学生分配到甲、乙、丙3个实验室准备实验,每个实验室至少分配1名学生的不同分配方案共有( )
| A、12种 | B、24种 |
| C、36种 | D、48种 |
设a>1>b>-1,则下列不等式一定成立的是( )
| A、a>b2 | ||||
| B、a2>2b | ||||
C、
| ||||
| D、|a|<|b| |
下列函数满足|x|≥|f(x)|的是( )
| A、f(x)=ex-1 |
| B、f(x)=ln(x+1) |
| C、f(x)=tanx |
| D、f(x)=sinx |
已知α为锐角,且cos(α+
)=
,则cosα的值为( )
| π |
| 6 |
| 4 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
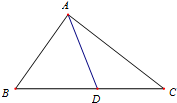 如图,在△ABC中,已知B=45°,D是BC上一点,AD=10,AC=14,DC=6,则AB=
如图,在△ABC中,已知B=45°,D是BC上一点,AD=10,AC=14,DC=6,则AB=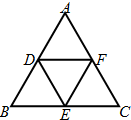 如图,已知D,E,F是正△ABC三边的中点,由A,B,C,D,E,F六点中的两点构成的向量中与
如图,已知D,E,F是正△ABC三边的中点,由A,B,C,D,E,F六点中的两点构成的向量中与