题目内容
若直线(2n+1)x+(n+5)y-6=0和(n-3)x+(1-2n)y-7=0垂直,则n的值为( )
A、
| ||
B、-
| ||
| C、1 | ||
D、
|
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:根据两条直线垂直,则x的系数之积加上y的系数之积等于零,列方程求出n的值.
解答:
解:∵直线(2n+1)x+(n+5)y-6=0和(n-3)x+(1-2n)y-7=0垂直,
∴(2n+1)•(n-3)+(n+5)•(1-2n)=0,
由此求得n=
,
故选:A.
∴(2n+1)•(n-3)+(n+5)•(1-2n)=0,
由此求得n=
| 1 |
| 7 |
故选:A.
点评:本题主要考查两直线垂直的性质,两条直线垂直,则x的系数之积加上y的系数之积等于零,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将4名学生分配到甲、乙、丙3个实验室准备实验,每个实验室至少分配1名学生的不同分配方案共有( )
| A、12种 | B、24种 |
| C、36种 | D、48种 |
下列函数满足|x|≥|f(x)|的是( )
| A、f(x)=ex-1 |
| B、f(x)=ln(x+1) |
| C、f(x)=tanx |
| D、f(x)=sinx |
已知p:xy=0,q:x=0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知α为锐角,且cos(α+
)=
,则cosα的值为( )
| π |
| 6 |
| 4 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
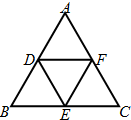 如图,已知D,E,F是正△ABC三边的中点,由A,B,C,D,E,F六点中的两点构成的向量中与
如图,已知D,E,F是正△ABC三边的中点,由A,B,C,D,E,F六点中的两点构成的向量中与