题目内容
已知在△ABC中满足:tanA•tanB=1+
(tanA+tanB),则角C等于( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:两角和与差的正切函数
专题:计算题,三角函数的求值
分析:根据tanA•tanB=1+
(tanA+tanB),可得tan(A+B)=
=-
,即可求出C.
| 3 |
| tanA+tanB |
| 1-tanAtanB |
| ||
| 3 |
解答:
解:∵tanA•tanB=1+
(tanA+tanB),
∴tan(A+B)=
=-
,
∴tanC=
,
∴C=
.
故选:A.
| 3 |
∴tan(A+B)=
| tanA+tanB |
| 1-tanAtanB |
| ||
| 3 |
∴tanC=
| ||
| 3 |
∴C=
| π |
| 6 |
故选:A.
点评:本题主要考查两角和的正切公式的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知a>0且a≠1,函数f(x)=
满足对任意实数x1≠x2,都有
>0成立,则a的取值范围是( )
|
| f(x2)-f(x1) |
| x2-x1 |
| A、(0,1) | ||
| B、(1,+∞) | ||
C、(1,
| ||
D、[
|
将函数y=
sinx+
cosx(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| 1 |
| 4 |
| ||
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
定义两种运算a⊕b=ab,a?b=a2+b2,则f(x)=
为( )
| 2⊕x |
| x?2-2 |
| A、奇函数 |
| B、偶函数 |
| C、既不是奇函数又不是偶函数 |
| D、既是奇函数又是偶函数 |
将4名学生分配到甲、乙、丙3个实验室准备实验,每个实验室至少分配1名学生的不同分配方案共有( )
| A、12种 | B、24种 |
| C、36种 | D、48种 |
已知α为锐角,且cos(α+
)=
,则cosα的值为( )
| π |
| 6 |
| 4 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
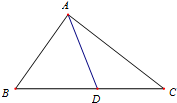 如图,在△ABC中,已知B=45°,D是BC上一点,AD=10,AC=14,DC=6,则AB=
如图,在△ABC中,已知B=45°,D是BC上一点,AD=10,AC=14,DC=6,则AB=