Question

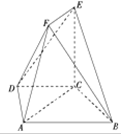如图所示的几何体，四边形ABCD中，有AB∥CD，∠BAC=30°，AB=2CD=2，CB=1．点E在平面ABCD内的射影是点C，EF∥AC，且AC=2EF．
（1）求证：平面BCE⊥平面ACEF；
（2）若二面角D-AF-C的平面角为60°，求CE的长．

Answer 1

考点：与二面角有关的立体几何综合题,平面与平面垂直的判定

专题：空间角

分析：（1）由已知条件利用余弦定理求出AC=

3

，由勾股定理得到BC⊥AC，由EC⊥平面ABCD，得到BC⊥EC，由此能够证明平面BCE⊥平面ACEF．
（2）以C为原点，建立空间直角坐标系，由二面角D-AF-C的平面角为60°，利用向量法能求出CE的长．

解答： （1）证明：在△ABC中，∵∠BAC=30°，AB=2CD=2，CB=1，
∴BC²=AB²+AC²-2AB•ACcos30°，
解得AC=

3

，∴AB²=AC²+BC²，
由勾股定理知∠ACB=90°，∴BC⊥AC，
∵EC⊥平面ABCD，BC?平面ABCD，∴BC⊥EC，
∵AC∩EC=C，∴BC⊥平面ACEF，
又BC?平面BCE，
∴平面BCE⊥平面ACEF．
（2）解：∵EC⊥平面ABCD，由（1）知BC⊥AC，
∴以C为原点，建立如图所示的空间直角坐标系，
设CE=h，则C（0，0，0），A（

3

，0，0），
F（

3

2

，0，h），D（

3

2

，-

1

2

，0），

AD

=（-

3

2

，-

1

2

，0），

AF

=（-

3

2

，0，h），
设平面DAF的法向量

n

=(x，y，z)，
则

n • AD =- 3 2 x- 1 2 y=0 n • AF =- 3 2 x+hz=0

，
令x=

3

，得

n

=（

3

，-3，

3

2h

），
又平面AFC的法向量

m

=（0，1，0），
∵二面角D-AF-C的平面角为60°，
∴|cos＜

n

，

m

＞|=|

-3

3+9+( 3 2h )2

|=cos60°=

1

2

，解得h=

6

8

，
∴CE的长为

6

8

．

点评：本题考查平面与平面垂直的证明，考查CE的长的求法，解题时要认真审题，注意向量法的合理运用．