题目内容
已知函数f(x)=(x-a)lnx,a∈R.若a=0,对于任意的x∈(0,1).
(1)求证:-
≤f(x)<2.
(2)若函数f(x)在其定义域内不是单调函数,求实数a的范围.
(1)求证:-
| 1 |
| e |
(2)若函数f(x)在其定义域内不是单调函数,求实数a的范围.
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)利用导数判断函数的单调性,求得函数的最值,即可得出结论;
(2)由题意可得,即证f′(x)=-alnx+
=
=0,即x-a(xlnx+1)=0,即a=
在x∈(0,1)有解即可,令g(x)=
,利用导数求得函数g(x)的最值,即可得出结论.
(2)由题意可得,即证f′(x)=-alnx+
| x-a |
| x |
| x-a(xlnx+1) |
| x |
| x |
| xlnx+1 |
| x |
| xlnx+1 |
解答:
解:(1)∵f(x)=(x-a)lnx,若a=0,则f(x)=xlnx,
∴f′(x)=lnx+1,
∴x∈(0,
)时,f′(x)<0,x∈(
,1)时,f′(x)>0,
∴当x=
时,f(x)min=f(
)=-
,
又f(1)=0,∴-
≤f(x)<0.
(2)∵f(x)=(x-a)lnx,
∴f′(x)=-alnx+
=
=0,
∴x-a(xlnx+1)=0,即a=
,x∈(0,1),
令g(x)=
,则g′(x)=
>0,
∴g(x)在(0,1)上单调递增,
∴0<g(x)<1,
又∵f(x)在其定义域内不是单调函数,
∴0<a<1.
∴f′(x)=lnx+1,
∴x∈(0,
| 1 |
| e |
| 1 |
| e |
∴当x=
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
又f(1)=0,∴-
| 1 |
| e |
(2)∵f(x)=(x-a)lnx,
∴f′(x)=-alnx+
| x-a |
| x |
| x-a(xlnx+1) |
| x |
∴x-a(xlnx+1)=0,即a=
| x |
| xlnx+1 |
令g(x)=
| x |
| xlnx+1 |
| 1-x |
| (xlnx+1)2 |
∴g(x)在(0,1)上单调递增,
∴0<g(x)<1,
又∵f(x)在其定义域内不是单调函数,
∴0<a<1.
点评:本题主要考查利用导数研究函数的单调性、极值、最值等知识,考查学生分析问题、解决问题的能力及转化划归思想的运用能力,属于难题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
已知函数f(x)=
,若a>0,b>0,c>0,a+b>c,则( )
| x |
| x+1 |
| A、f(a)+f(b)>f(c) |
| B、f(a)+f(b)=f(c) |
| C、f(a)+f(b)<f(c) |
| D、以上结论都不对 |
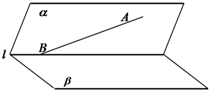 如图,已知二面角α-l-β的大小是60°,线段AB∈α.B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是
如图,已知二面角α-l-β的大小是60°,线段AB∈α.B∈l,AB与l所成的角为30°,则AB与平面β所成的角的正弦值是